题目内容
14．分式计算（1）$\frac{a+1}{{{a^2}-a}}÷\frac{{{a^2}-1}}{{{a^2}-2a+1}}$
（2）$\frac{{{a^2}-1}}{{{a^2}-5a+6}}÷\frac{{{a^2}+a-2}}{a-3}-\frac{a+3}{{{a^2}-4}}$．
分析 （1）分子、分母先因式分解，然后约分化简即可．
（2）先计算除法，后计算加减，最后通分化简即可．
解答 解：（1）原式=$\frac{a+1}{a（a-1）}$•$\frac{（a-1）^{2}}{（a+1）（a-1）}$=$\frac{1}{a}$
（2）原式=$\frac{（a+1）（a-1）}{（a-2）（a-3）}$•$\frac{a-3}{（a+2）（a-1）}$-$\frac{a+3}{（a+2）（a-2）}$=$\frac{a+1}{（a-2）（a+2）}$-$\frac{a+3}{（a+2）（a-2）}$=$-\frac{2}{{{a^2}-4}}$
点评 本题考查分式的混合运算，解题的关键是熟练掌握分式的混合运算法则，注意运算顺序，属于中考常考题型．
练习册系列答案
相关题目
4．已知两个质地均匀的正方体A，B，每个面上分别标有数字1，2，3，4，5，6，同时抛掷A，B，设两立方体朝上的数字分别为x，y，并以此确定点P（x，y），那么点P落在抛物线y=-x2+3x上的概率为（ ）
| A． | $\frac{1}{18}$ | B． | $\frac{1}{12}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{6}$ |
5．
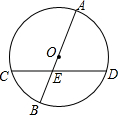如图，AB为⊙O的直径，CD为弦，AE=7cm，BE=3cm，∠AED=60°，则弦CD的长为（ ）
如图，AB为⊙O的直径，CD为弦，AE=7cm，BE=3cm，∠AED=60°，则弦CD的长为（ ）| A． | 2$\sqrt{21}$cm | B． | 4$\sqrt{6}$cm | C． | 2$\sqrt{22}$cm | D． | 8cm |
2．元旦期间，为了满足长丰县百姓的消费需要，某大型商场计划用170000元购进一批家电，这批家里的进价和售价如表：
若在现有资金允许的范围内，购买表中三类家电共100台，其中彩电台数是冰箱台数的2倍，设该商场购买冰箱x台．
（1）用含x的代数式表示洗衣机的台数．
（2）商场至多可以购买冰箱多少台？
（3）购买冰箱多少台时，能使商场销售完这批家电后获得的利润最大？最大利润为多少元？
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价（元/台） | 2000 | 1600 | 1000 |
| 售价（元/台） | 2300 | 1800 | 1100 |
（1）用含x的代数式表示洗衣机的台数．
（2）商场至多可以购买冰箱多少台？
（3）购买冰箱多少台时，能使商场销售完这批家电后获得的利润最大？最大利润为多少元？
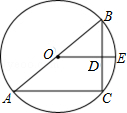如图，AB是⊙O的直径，BC是弦，点E是BC的中点，OE交BC于点D．连接AC，若BC=6，DE=1，求AC的长．
如图所示，在由边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在网格线的交点上，则∠AED的正切值等于$\frac{1}{2}$．