题目内容
16. 如图,一副三角板如图放置,已知∠2比∠1的补角的2倍小5°,则∠1=145°.
如图,一副三角板如图放置,已知∠2比∠1的补角的2倍小5°,则∠1=145°.
分析 根据三角板的种类,可得∠3=90°,∠4=60°,再由周角为360°即可求得答案.
解答 解: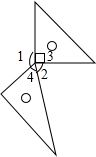
由图形可得:∠3=90°,∠4=60°,
则∠1+∠2=210°,2∠1+∠2=355
又∵∠2比∠1的补角的2倍小5°,
∴可得:$\left\{\begin{array}{l}{∠1+∠2=210°}\\{2(180°-∠1)=∠2+5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{∠1=145°}\\{∠2=65°}\end{array}\right.$.
故答案为:145°.
点评 本题考查了余角和补角的知识,解答本题的关键是熟练三角板的种类,找到隐含条件.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
6.下列计算正确的是( )
| A. | a+3a=4a2 | B. | a4•a4=2a4 | C. | (a2)3=a5 | D. | (-a)3÷(-a)=a2 |
4.下列对平移的描述正确的是( )
| A. | 坐在秋千上的人的运动是平移 | |
| B. | 把一个20°的角向右平移2个单位后度数为40° | |
| C. | 水平线段AB=2cm,向上平移2个单位后得线段CD,则CD∥AB,且CD=2cm | |
| D. | 同一个人手心朝上的两只手,左手可以通过平移与右手重合 |
11.若代数式3a+2b-4的值为2,那么代数式9a+6b-11的值为( )
| A. | 29 | B. | -17 | C. | 7 | D. | 5 |
 如图,已知在△ABC中,AD=BD,BE=CE,AF=CF.求证:AE,DF互相平分.
如图,已知在△ABC中,AD=BD,BE=CE,AF=CF.求证:AE,DF互相平分.