题目内容
7.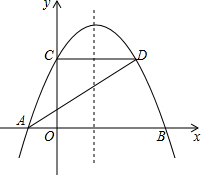 如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).
如图,已知抛物线y=ax2+$\frac{4}{3}$x+c与x轴交于A、B两点,与y轴交于点C,点D在抛物线上,且A(-1,0),D(2,2).(1)求这条抛物线的解析式;
(2)在y轴上是否存在点P,使以O、B、P为顶点的三角形与△AOC相似?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)小明在探索该图时提出了这样一个猜想:“直线AD平分∠CAB”,你认为小明的猜想正确吗?请说明理由.
分析 (1)根据待定系数法,可得抛物线的解析式;
(2)根据两组对边对应成比例且夹角相等的两个三角形相似,可得关于OP的方程,根据解方程,可得答案;
(3)根据角平分线的性质,平行线的性质,可得∠CAD=∠CDA,根据等腰三角形的判定,可得AC与CD的关系,根据勾股定理,可得AC的长,根据有理数的大小比较,可得AC与CD的关系.
解答 解:(1)∵抛物线y=ax2+$\frac{4}{3}$x+c过A、D两点,
将A(-1,0),D(2,2)代入抛物线解析式中,
得$\left\{\begin{array}{l}{a-\frac{4}{3}+c=0}\\{4a+\frac{8}{3}+c=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{c=2}\end{array}\right.$
∴抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2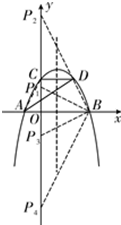
(2)存在这样的点P,使以O、B、P为顶点的三角形与△AOC相似,
连接AC,由y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2,C(0,2),B(3,0),
∵∠AOC=∠BOP=90°
①当$\frac{OA}{OP}$=$\frac{OC}{OB}$时,即$\frac{1}{OP}$=$\frac{2}{3}$,
解得OP=$\frac{3}{2}$,即P1(0,$\frac{3}{2}$),P3(0,-$\frac{3}{2}$)此时△AOC∽△POB,
②$\frac{OA}{OB}$=$\frac{OC}{OP}$时,即$\frac{1}{3}$=$\frac{2}{OP}$,
解得OP=6,即P2(0,6),P4(0,-6),此时△AOC∽△BOP,
∴y轴上存在这样的P点,P1(0,$\frac{3}{2}$),P3(0,-$\frac{3}{2}$),P2(0,6),P4(0,-6);
(3)小明的猜想不正确.理由如下:
若AD平分∠CAB,
则∠CAD=∠BAD.
又∵CD∥x轴,
∴∠CDA=∠DAB,
∴∠CAD=∠CDA,
∴CA=CD.
实际上:CD=2,CA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
即CD≠CA,
∴猜想不正确.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用相似三角形的判定得出关于OP的方程是解题关键,要分类讨论,以防遗漏;利用了平行线的性质,角平分线的性质,等腰三角形的判定.

 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )| A. | -4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
 已知x轴上两点A(-1,0)、B(4,0).
已知x轴上两点A(-1,0)、B(4,0).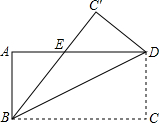 如图,把矩形ABCD沿直线BD向上折叠,使点C落在C′的位置上,已知AB=3,BC=7,重合部分△EBD的面积为$\frac{87}{14}$.
如图,把矩形ABCD沿直线BD向上折叠,使点C落在C′的位置上,已知AB=3,BC=7,重合部分△EBD的面积为$\frac{87}{14}$.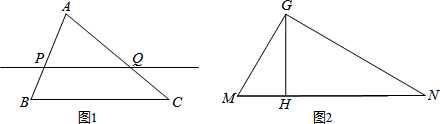
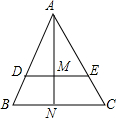 如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.
如图,已知△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90.求△ADE的面积及AM、AN的长.