题目内容
13. 如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )| A. | -12 | B. | 12 | C. | 16 | D. | 18 |
分析 由PB∥OC可得出△PBQ∽△COQ,结合三角形面积比等于相似比的平方可得出PB=PA=$\frac{1}{2}$OC,结合正方形OABC的边长为6可得出点C、点P的坐标,利用待定系数法即可求出直线CP的函数解析式,联立直线OB与直线CP的函数解析式即可得出点Q的坐标,利用待定系数法即可求出k值.
解答 解:∵PB∥OC(四边形OABC为正方形),
∴△PBQ∽△COQ,
∴$\frac{{S}_{△BPQ}}{{S}_{△OQC}}$=$(\frac{PB}{OC})^{2}$=$\frac{1}{4}$,
∴PB=PA=$\frac{1}{2}$OC=3.
∵正方形OABC的边长为6,
∴点C(0,6),点P(6,3),直线OB的解析式为y=x①,
∴设直线CP的解析式为y=ax+6,
∵点P(6,3)在直线CP上,
∴3=6a+6,解得:a=-$\frac{1}{2}$,
故直线CP的解析式为y=-$\frac{1}{2}$x+6②.
联立①②得:$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}x+6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
∴点Q的坐标为(4,4).
将点Q(4,4)代入y=$\frac{k}{x}$中,得:
4=$\frac{k}{4}$,解得:k=16.
故选C.
点评 本题考查了反比例函数系数k的几何意义以及待定系数法求函数解析式,解题的关键是求出点Q的坐标.本题属于基础题,难度不大,解决该题型题目时,根据相似三角形的面积比等于相似比的平方结合给定条件求出点Q的坐标,再利用待定系数法求出反比例函数解析式即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-2的相反数的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
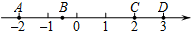 如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
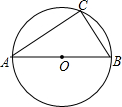 如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(
如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(| A. | 4 | B. | 5 | C. | $\frac{40}{9}$ | D. | $\frac{15}{4}$ |
 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )| A. | 59° | B. | 31° | C. | 124° | D. | 121° |
 如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.
如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=6.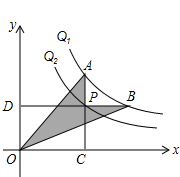 如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.
如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.