题目内容
17.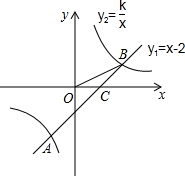 如图,一次函数y1=x-2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$,点B的坐标为(m,n),求反比例函数的解析式.
如图,一次函数y1=x-2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$,点B的坐标为(m,n),求反比例函数的解析式.
分析 过点B作BD⊥x轴于点D,由点B的坐标结合tan∠BOC=$\frac{1}{2}$可得出m与n的关系,将点B坐标代入一次函数y1=x-2中可得出关于m、n的二元一次方程,结合前面得出的m、n之间的关系即可得出点B的坐标,再由点B的坐标结合待定系数法即可求出反比例函数的解析式.
解答 解:过点B作BD⊥x轴于点D,如图1所示.
则BD=n,OD=m.
∵tan∠BOD=$\frac{BD}{OD}=\frac{n}{m}$=$\frac{1}{2}$,
∴m=2n.
又∵点B在直线y1=x-2上,
∴n=m-2.
∴n=2n-2,解得:n=2,
则m=4.
∴点B的坐标为(4,2).
将(4,2)代入y2=$\frac{k}{x}$得,$\frac{k}{4}$=2,
∴k=8.
∴反比例函数的解析式为y2=$\frac{8}{x}$.
点评 本题考查了反比例函数与一次函数交点的问题以及待定系数法求函数解析式,解题的关键是求出点B的坐标.本题属于基础题,解决该题型题目时,根据已知条件求出点B的坐标,再结合待定系数法去求出反比例函数解析式.

练习册系列答案
相关题目
5.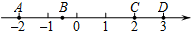 如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )
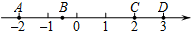 如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中绝对值小于2的数对应的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
2.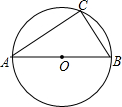 如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(
如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(
 如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(
如图,AB为圆O的直径,在圆O上取异于A、B的一点C,并连结BC、AC.过点A作圆O的切线,交直线BC于点D,作∠ADC的角平分线,交AB于点P.若AB=10,BC=6,则AP的长度为(| A. | 4 | B. | 5 | C. | $\frac{40}{9}$ | D. | $\frac{15}{4}$ |
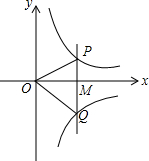 如图,若点M是x轴正半轴上的任意一点,过点M作PQ⊥x轴,分别交函数y=$\frac{4}{x}$(x>0)和y=-$\frac{6}{x}$(x>0)的图象于点P和Q,连接OP、OQ,则△POQ的面积为5.
如图,若点M是x轴正半轴上的任意一点,过点M作PQ⊥x轴,分别交函数y=$\frac{4}{x}$(x>0)和y=-$\frac{6}{x}$(x>0)的图象于点P和Q,连接OP、OQ,则△POQ的面积为5.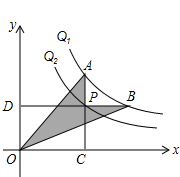 如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.
如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.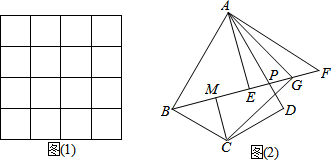
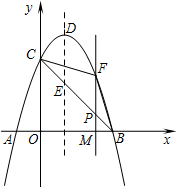 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.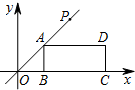 如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )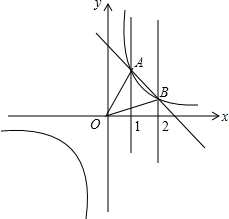 已知一次函数y1=-x+3与反比例函数y2=$\frac{2}{x}$的图象交于点A(1,2),B(2,1).
已知一次函数y1=-x+3与反比例函数y2=$\frac{2}{x}$的图象交于点A(1,2),B(2,1).