题目内容
19．（1）先化简，再求代数式的值：（1-$\frac{1}{m+2}$）÷$\frac{{m}^{2}+2m+1}{{m}^{2}-4}$，其中m=1．（2）解方程：$\frac{1}{x+2}$+$\frac{1}{2x-1}$=0．
分析 （1）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把m的值代入计算即可求出值；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=$\frac{m+1}{m+2}$•$\frac{（m+2）（m-2）}{（m+1）^{2}}$=$\frac{m-2}{m+1}$，
当m=1时，原式=-$\frac{1}{2}$；
（2）去分母得：2x-1+x+2=0，
解得：x=-$\frac{1}{3}$，
经检验x=-$\frac{1}{3}$是分式方程的解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
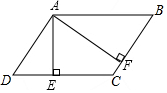如图，在平行四边形ABCD中，AE⊥CD，垂足为E，AF⊥BC，垂足为F，AD=4，BF=3，∠EAF=60°，设$\overrightarrow{AB}$=$\overrightarrow{a}$，如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$（k≠0），那么k的值是-$\frac{2}{3}$．
如图，正方形OABC的边长为2，点A在x轴上，点C在y轴上，函数y=-$\frac{2}{3}$x2+bx+c的图象经过点B和点C，直线CA交抛物线于点P，PQ⊥x轴于点Q．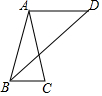
如图，已知AB=AC=AD，且∠C=2∠D，求证AD∥BC．