题目内容
4. 如图,正方形OABC的边长为2,点A在x轴上,点C在y轴上,函数y=-$\frac{2}{3}$x2+bx+c的图象经过点B和点C,直线CA交抛物线于点P,PQ⊥x轴于点Q.
如图,正方形OABC的边长为2,点A在x轴上,点C在y轴上,函数y=-$\frac{2}{3}$x2+bx+c的图象经过点B和点C,直线CA交抛物线于点P,PQ⊥x轴于点Q.(1)求该二次函数的解析式;
(2)x取何值时y>0?
(3)求$\frac{CA}{AP}$.
分析 (1)由正方形的性质可求得B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可求得抛物线与x轴的交点,结合抛物线可求得x的取值范围;
(3)由A、C坐标可求得直线AC的解析式,联立直线AC与抛物线的解析式可求得P点坐标,从而可求得PQ的长,又由△AOC∽△AQP,利用相似三角形的性质可求得答案.
解答 解:
(1)∵正方形OABC的边长为2,
∴B(2,2),C(0,2),
把B、C的坐标代入抛物线解析式可得$\left\{\begin{array}{l}{-\frac{2}{3}×{2}^{2}+2b+c=2}\\{c=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{4}{3}}\\{c=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2;
(2)在y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2中,令y=0可得0=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2,解得x=-1或x=3,
∵抛物线开口向下,
∴当-1<x<3时,y>0;
(3)∵A(2,0),C(0,2),
∴直线AC的解析式为y=-x+2,
联立直线AC与抛物线解析式可得$\left\{\begin{array}{l}{y=-x+2}\\{y=-\frac{2}{3}{x}^{2}+\frac{4}{3}x+2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$,
∴P点坐标为($\frac{7}{2}$,-$\frac{3}{2}$),
∴AQ=PQ=$\frac{3}{2}$,
∴△APQ是等腰直角三角形,△AOC为等腰直角三角形,
∴CA=$\sqrt{2}$OA=2$\sqrt{2}$,AP=$\sqrt{2}$AQ=$\frac{3\sqrt{2}}{2}$,
∴$\frac{CA}{AP}$=$\frac{2\sqrt{2}}{\frac{3\sqrt{2}}{2}}$$\frac{4}{3}$.
点评 本题为二次函数的综合应用,涉及待定系数法、正方形的性质、一元二次方程、函数图象的交点、勾股定理、方程思想及数形结合思想等知识.在(1)中求得B、C的坐标是解题的关键,在(2)中求得抛物线与x轴的交点坐标是解题的关键,在(3)中求得P点坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.

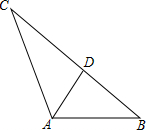 从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线. 如图,将一张长方形的纸片ABCD沿AF折叠,点B到达点B′的位置.已知AB′∥BD,∠ADB=20°,则∠BAF=55°.
如图,将一张长方形的纸片ABCD沿AF折叠,点B到达点B′的位置.已知AB′∥BD,∠ADB=20°,则∠BAF=55°.