题目内容
8.已知:△ABC内接于⊙O,直径AM平分∠BAC.(1)如图1,求证AB=AC;
(2)如图2,弦FG分别交AB、AC于点D、E,AE=BD,当∠ADE+∠DEC=90°时,连接CD,直径AM分别交DE、CD、BC于N、H、R,若CD⊥AB,求证:∠NDC=∠ACB;
(3)在(2)的条件下,若DE长为$\sqrt{2}$,求△ACH的面积.
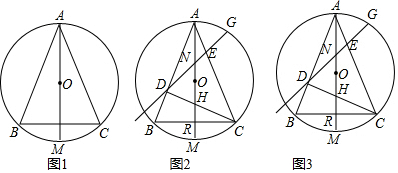
分析 (1)如图1中,分别过点O作OP⊥AB于P,OQ⊥AC于Q,只要证明△OAP≌△OAQ即可解决问题.
(2)如图2中,作DS⊥AC于S,想办法证明∠NDC=∠ACB=67.5°即可解决问题.
(3)过点E作EK∥AB交AM于K.首先证明四边形EKBD是平行四边形,由△ADE≌△ECK,推出DE=KC,由DE=BK,推出KB=KC,由∠BKM=∠DNM=45°,推出∠BKC=90°推出BC=$\sqrt{2}$BK=$\sqrt{2}$DE=2,由△ADH≌△CDB,推出AH=BC=2,BR=CR=1,根据S△ACH=$\frac{1}{2}$•AH•CR计算即可.
解答 (1)证明:如图1中,分别过点O作OP⊥AB于P,OQ⊥AC于Q,
∴AP=PB=$\frac{1}{2}$AB,AQ=CQ=$\frac{1}{2}$AC,
∵AM平分∠BAC
∴OP=OQ,
∵OA=OA,
∴△OAP≌△OAQ,
∴AP=AQ,
∴AB=AC.
(2)如图2中,作DS⊥AC于S.
∵∠CED=90°-∠ADE=90°-∠EDS,
∴∠ADE=∠EDS,
∵∠ADE+∠DEC=90°,
又∵∠ADE+∠CDE=90°,
∴∠CDE=∠DEC,
∴CD=CE,
∴∠CDE=∠CED,
∴∠ADS=∠EDS,
∵∠DAS+∠ADS=90°,
∴∠DAN+∠ADN=45°,
∴∠DNM=45°,
∵AD=CE,
∴AD=DC,
∴∠DAC=45°,
∴∠DAM=22.5°,∠ADN=22.5°,
∴∠NDC=67.5°
∵∠CAM=22.5°,
∴∠ACB=67.5°,
∴∠NDC=∠ACB.
(3)过点E作EK∥AB交AM于K.
∵∠BAM=∠CAM,
∴∠EKA=∠BAM=∠CAM,
∴EK=AE,
∴EK=BD
∴四边形EKBD是平行四边形,
∵AD=CE,∠DAE=∠KEC,AE=EK,
∴△ADE≌△ECK,
∴DE=KC,∵DE=BK,
∴KB=KC,
∵∠BKM=∠DNM=45°,
∴∠BKC=90°
∴BC=$\sqrt{2}$BK=$\sqrt{2}$DE=2,
∵△ADH≌△CDB,
∴AH=BC=2,BR=CR=1
∴S△ACH=$\frac{1}{2}$•AH•CR=$\frac{1}{2}$×2×1=1.
点评 本题考查圆综合题、全等三角形的判定和性质、平行四边形的判定和性质、等腰三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题时根据是学会添加常用辅助线,构造全等三角形或特殊四边形解决问题,属于中考压轴题.

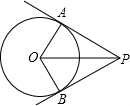 如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )
如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )| A. | 90° | B. | 100° | C. | 110° | D. | 60° |
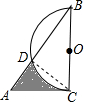 如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.
如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.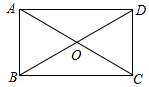 如图,在矩形ABCD中,∠ABD=60°,AB=4,则AC=8.
如图,在矩形ABCD中,∠ABD=60°,AB=4,则AC=8.