题目内容
8.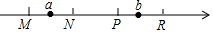 如图M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1,数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=2,则原点是N或P(填入M、N、P、R中的一个或几个).
如图M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1,数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=2,则原点是N或P(填入M、N、P、R中的一个或几个).
分析 根据数轴判断出a、b之间的距离小于3,且大于1,然后根据绝对值的性质解答即可.
解答  解:∵MN=NP=PR=1,
解:∵MN=NP=PR=1,
∴|MN|=|NP|=|PR|=1,
∴|MR|=3;
①当原点在N或P点时,1<|a|+|b|<3,又因为|a|+|b|=2,所以原点可能在N或P点;
②当原点在M或R点时,|a|+|b|>2,所以原点不可能在M或R点;
综上所述,原点应是在N或P点.
故答案为:N或P.
点评 此题考查了数轴的定义和绝对值的意义.解此类题的关键是:先利用条件判断出绝对值符号里代数式的正负性,再根据绝对值的性质把绝对值符号去掉,把式子化简后根据整点的特点求解.

练习册系列答案
相关题目
17.若关于x的方程x2-$\sqrt{2}$x+cosα=0有两个相等实数根,则锐角α的度数为( )
| A. | 60° | B. | 45° | C. | 30° | D. | 22.5° |
 如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.
如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E. 如图,直线l1过点A(0,-5),点B(5,0),直线l2与x轴交于点C(-1,0),与y轴交于点D(0,-1),两直线l1,l2相交于点P,求△PAD的面积是4.
如图,直线l1过点A(0,-5),点B(5,0),直线l2与x轴交于点C(-1,0),与y轴交于点D(0,-1),两直线l1,l2相交于点P,求△PAD的面积是4.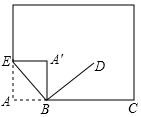 如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由.
如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由. 如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.
如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.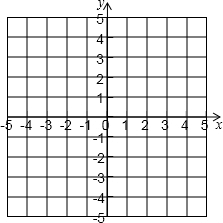 在平面直角坐标系中,将坐标是(0,4),(1,0),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
在平面直角坐标系中,将坐标是(0,4),(1,0),(3,0),(4,4)的点用线段依次连接起来形成一个图案. 