题目内容
5.解方程:(1)$\frac{4}{x-1}$+$\frac{2x-1}{1-x}$=1;
(2)$\frac{4}{x+1}$+$\frac{5}{x-1}$=$\frac{10}{{x}^{2}-1}$;
(3)$\frac{1}{2-x}$=$\frac{1}{x-2}$-$\frac{6-x}{3{x}^{2}-12}$.
分析 各分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:4-2x+1=x-1,
解得:x=2,
经检验x=2是分式方程的解;
(2)去分母得:4x-4+5x+5=10,
解得:x=1,
经检验x=1是增根,分式方程无解;
(3)去分母得:-3(x+2)=3(x+2)-6+x,
去括号得:-3x-6=3x+6-6+x,
解得:x=-$\frac{6}{7}$,
经检验x=-$\frac{6}{7}$是分式方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
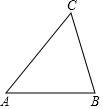 如图,已知△ABC.
如图,已知△ABC. 在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上). 如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD.
如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD.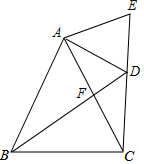 如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )
如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( ) 如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.
如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.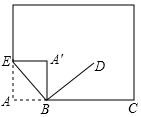 如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由.
如图所示,小明将书面折过来,该角顶点A落在A′处,他以折痕BE为一边作∠DBE=90°,此时小明说BD是∠CBA′的平分线.你认为小明的说法对吗?说明你的理由.