题目内容
12. 如图,已知△ABC内接于圆O,$\widehat{AB}$=$\widehat{AC}$,tanB=$\frac{1}{2}$,求$\frac{AB}{BC}$的值.
如图,已知△ABC内接于圆O,$\widehat{AB}$=$\widehat{AC}$,tanB=$\frac{1}{2}$,求$\frac{AB}{BC}$的值.
分析 连接AO交BC于D,根据垂径定理得到AD⊥BC,BC=2BD,设AD=k,BD=2k,根据勾股定理得到AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{5}$k,于是得到结论.
解答 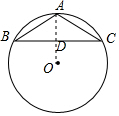 解:连接AO交BC于D,
解:连接AO交BC于D,
∵$\widehat{AB}$=$\widehat{AC}$,
∴AD⊥BC,BC=2BD,
∵tanB=$\frac{1}{2}$,
∴$\frac{AD}{BD}$=$\frac{1}{2}$,
∴设AD=k,BD=2k,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{5}$k,
∴BC=4k,
∴$\frac{AB}{BC}$=$\frac{\sqrt{5}}{4}$.
点评 本题考查了垂径定理,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
2.某公司准备把240吨白砂糖运往A、B两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见表:
(1)求大、小两种货车各用多少辆?
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
| 载重量 | 运往A地的费用 | 运往B地的费用 | |
| 大车 | 15吨/辆 | 630元/辆 | 750元/辆 |
| 小车 | 10吨/辆 | 420元/辆 | 550元/辆 |
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
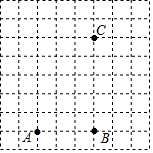 如图所示,已知点A、B、C是网格纸上的三个格点,根据要求画图或作答.
如图所示,已知点A、B、C是网格纸上的三个格点,根据要求画图或作答.
 如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD.
如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD. 如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.
如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.
 如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.
如图中的四边形均为矩形,根据图形,仅用图中出现的字母写出一个正确的等式:m(a+b+c)=ma+mb+mc.