题目内容
 如图,⊙O的半径为5,∠PAQ=90°,AP切⊙O于点T,AQ交O于B,C点.
如图,⊙O的半径为5,∠PAQ=90°,AP切⊙O于点T,AQ交O于B,C点.(1)求证:BT平分∠ABO;
(2)AT=4,请求出AB的长.
考点:切线的性质
专题:
分析:(1)连接OT,求出AB∥OT,推出∠TBA=∠BTO,求出∠OBT=∠TBA,即可得出答案;
(2)过点B作BH⊥OT于H,根据勾股定理求出OH,代入AB=HT=OT-OH求出即可.
(2)过点B作BH⊥OT于H,根据勾股定理求出OH,代入AB=HT=OT-OH求出即可.
解答:(1)证明:连接OT,
∵AT是切线,
∴OT⊥AP,
∵∠PAB是直角,即AQ⊥AP,
∴AB∥OT,
∴∠TBA=∠BTO,
∵OT=OB,
 ∴∠OTA=∠OBT,
∴∠OTA=∠OBT,
∴∠OBT=∠TBA,
即BT平分∠OBA;
(2)解:过点B作BH⊥OT于H,
则在Rt△OBH中,OB=5,BH=AT=4,由勾股定理得:OH=3,
则AB=HT=5-3=2.

∵AT是切线,
∴OT⊥AP,
∵∠PAB是直角,即AQ⊥AP,
∴AB∥OT,
∴∠TBA=∠BTO,
∵OT=OB,
 ∴∠OTA=∠OBT,
∴∠OTA=∠OBT,∴∠OBT=∠TBA,
即BT平分∠OBA;
(2)解:过点B作BH⊥OT于H,
则在Rt△OBH中,OB=5,BH=AT=4,由勾股定理得:OH=3,
则AB=HT=5-3=2.
点评:本题考查了平行线的性质和判定,切线的性质,勾股定理,矩形的性质和判定的应用,注意:圆的切线垂直于过切点的半径,题目综合性比较强,难度适中.

练习册系列答案
相关题目
一个容量为50的样本中,数据的最大值是123,最小值是45,若取每组终点值与起点值的差为10,则该样本可以分( )
| A、5组或6组 |
| B、6组或7组 |
| C、7组或8组 |
| D、8组或9组 |
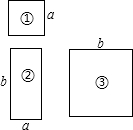 如图所示,现有边长分别为b、a的正方形、邻边长为b和a(b>a)的长方形硬纸板若干.
如图所示,现有边长分别为b、a的正方形、邻边长为b和a(b>a)的长方形硬纸板若干.
 如图,菱形ABCD的边长为12cm,∠A=60°,点P从点A出发沿线路AB→BD做匀速运动,点Q从点D同时出发沿线路DC→CB→BA做匀速运动.已知点P,Q运动的速度分别为2cm/秒和2.5cm/秒,经过12秒后,P、Q分别到达M、N两点时,点P、Q再分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改为vcm/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与△AMN相似,则v的值为
如图,菱形ABCD的边长为12cm,∠A=60°,点P从点A出发沿线路AB→BD做匀速运动,点Q从点D同时出发沿线路DC→CB→BA做匀速运动.已知点P,Q运动的速度分别为2cm/秒和2.5cm/秒,经过12秒后,P、Q分别到达M、N两点时,点P、Q再分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改为vcm/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与△AMN相似,则v的值为 如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于多少?
如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于多少?