题目内容
16.在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,⊙O是Rt△ABC的内切圆,则⊙O的面积是4πcm2(用含π的式子表示).分析 首先求出AB的长,再连圆心和各切点,利用切线长定理用半径表示AF和BF,而它们的和等于AB,得到关于r的方程,解方程求出半径,再求出圆的面积即可.
解答 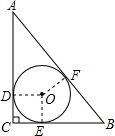 解:连OD,OE,OF,如图所示,
解:连OD,OE,OF,如图所示,
设半径为r.则OE⊥BC,OF⊥AB,OD⊥AC,CD=r.
∵∠C=90°,BC=5cm,AC=12cm,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=13cm,
∴BE=BF=(5-r)cm,AF=AD=(12-r)cm,
∴5-r+12-r=13,
∴r=2.即Rt△ABC的内切圆半径为2cm
∴△ABC的内切圆⊙O的面积=π×22=4π(cm2),
故答案为:4πcm2.
点评 此题主要考查了勾股定理以及直角三角形内切圆半径求法等知识,熟练掌握切线长定理和勾股定理.此题让我们记住一个结论:直角三角形内切圆的半径等于两直角边的和与斜边的差的一半.

练习册系列答案
相关题目
11.将半径为6,圆心角为120°的一个扇形围成一个圆锥(不考虑接缝),则圆锥的底面直径是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
8.方程x-5=3x+7移项后正确的是( )
| A. | x+3x=7+5 | B. | x-3x=-5+7 | C. | x-3x=7-5 | D. | x-3x=7+5 |