题目内容
9.三个同学对问题“若方程组$\left\{\begin{array}{l}{{a}_{1}x{+b}_{1}y{=c}_{1}}\\{{a}_{2}x{+b}_{2}y{=c}_{2}}\end{array}\right.$ 的解是$\left\{\begin{array}{l}{x=4}\\{y=10}\end{array}\right.$,求方程组$\left\{\begin{array}{l}{{4a}_{1}x+{5b}_{1}y={9c}_{1}}\\{{4a}_{2}x+{5b}_{2}y={9c}_{2}}\end{array}\right.$的解”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组中两个方程的两边都除以9,通过换元替代的方法来解决”,参照他们的讨论,你认为这个题目的解应该是?分析 根据等式的性质,可把第二个方程组化成第一个方程组的形式,根据相同的方程组的解也相同,可得关于x、y的二元一次方程,根据解方程组,可得答案.
解答 解:$\left\{\begin{array}{l}{{4a}_{1}x+{5b}_{1}y={9c}_{1}}\\{{4a}_{2}x+{5b}_{2}y={9c}_{2}}\end{array}\right.$,
方程组的每一个方程两边都除以9,得$\left\{\begin{array}{l}{{a}_{1}•\frac{4}{9}x+{b}_{1}•\frac{5}{9}y={c}_{1}}\\{{a}_{2}•\frac{4}{9}x+{b}_{2}•\frac{5}{9}y={c}_{2}}\end{array}\right.$,
∵方程组$\left\{\begin{array}{l}{{a}_{1}x{+b}_{1}y{=c}_{1}}\\{{a}_{2}x{+b}_{2}y{=c}_{2}}\end{array}\right.$ 的解是$\left\{\begin{array}{l}{x=4}\\{y=10}\end{array}\right.$,
∴$\left\{\begin{array}{l}{\frac{4}{9}x=4}\\{\frac{5}{9}y=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=9}\\{y=18}\end{array}\right.$.
点评 本题考查了二元一次方程组的解,根据等式的性质把第二个方程组化成第一个方程组的形式是解题关键.

练习册系列答案
相关题目
19.一次同学聚会,小李、小王、小明、小红4人见面,若他们每两人之间总要握手一次,则一共握手的次数是( )
| A. | 4次 | B. | 6次 | C. | 8次 | D. | 10次 |
14.现规定一种运算“∧”,x∧y=2x•2y,如3∧2=23•22=25=32,则4∧8的结果是( )
| A. | 211 | B. | 212 | C. | 232 | D. | 32 |
8. 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\frac{{\sqrt{15}}}{5}$或$\frac{{\sqrt{15}}}{3}$ | D. | 以上都不对 |
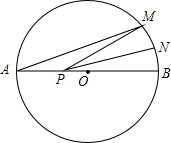 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5.
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5.