Question

19．如图，在平面直角坐标系xOy中，直线l：y=kx-3k（k＜0）与x、y轴的正半轴分别交于点A、B，动点D（异于点A、B）在线段AB上，DC⊥x轴于C．
（1）不论k取任何负数，直线l总经过一个定点，写出该定点的坐标为（3，0）；
（2）当点C的横坐标为2时，在x轴上存在点P，使得PB⊥PD，则k的取值范围为-$\frac{\sqrt{3}}{3}≤k＜0$．

Answer 1

分析 （1）在y=kx-3k（k＜0）中，当y=0时，x=3，即：不论k取任何负数，直线l总经过定点（3，0）．
（2）可设点P的坐标为（a，0），证明△BOP∽△PCD，由$\frac{BO}{PC}=\frac{OP}{CD}$分析k的取值范围．

解答 解：（1）∵y=kx-3k=k（x-3），
又∵k≠0，
∴x-3=0，即：x=3
∴x=3时，y=0，
即不论k取任何负数，直线l总经过定点（3，0），
故答案为：（3，0），
（2）设点P的坐标为（a，0），
∵OB⊥OA，PB⊥PD，DC⊥OA，
∴∠BOP=∠PCD=90°，∠BPD=90°，
∴∠BPO+∠DPC=90°，
又∵∠BPO+∠PBO=90°，
∴PBO=∠DPC，
∴△BOP∽△PCD，
∴$\frac{BO}{PC}=\frac{OP}{CD}$，
∵y=kx-3k，点P（a，0），点A（3，0），
∴x=0时，y=-3k，OP=a，PC=2-a，CD=2k-3k=-k，
∴BO=-3k，
∴$\frac{-3k}{2-a}=\frac{a}{-k}$
解得，3k²=2a-a²
∴a²-2a+1=1-3k²
∴（a-1）²=1-3k²
∵（a-1）²≥0，
∴1-3k²≥0
∴-$\frac{\sqrt{3}}{3}$$≤k≤\frac{\sqrt{3}}{3}$，
又∵k＜0，
∴-$\frac{\sqrt{3}}{3}≤k＜0$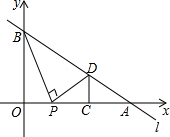

点评 本题考查了一次函数图象上点的坐标特征、相似三角形的判定与性质，解题的关键证明△BOP∽△PCD，由$\frac{BO}{PC}=\frac{OP}{CD}$分析k的取值范围