题目内容
12. 如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
如图,平行四边形ABCD中,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AE的长.
分析 (1)由平行四边形的性质和AAS证明△OBE≌△ODF,得出对应边相等即可;
(2)证出AE=GE,再证明DG=DO,得出OF=FG=1,即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠OBE=∠ODF.
在△OBE与△ODF中,
$\left\{\begin{array}{l}∠OBE=∠ODF\\∠BOE=∠DOF\\ BE=DF\end{array}\right.$
∴△OBE≌△ODF(AAS).
∴BO=DO.
(2)解:∵EF⊥AB,AB∥DC,
∴∠GEA=∠GFD=90°.
∵∠A=45°,
∴∠G=∠A=45°.
∴AE=GE
∵BD⊥AD,
∴∠ADB=∠GDO=90°.
∴∠GOD=∠G=45°.
∴DG=DO,
∴OF=FG=1,
由(1)可知,OE=OF=1,
∴GE=OE+OF+FG=3,
∴AE=3.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题(1)的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.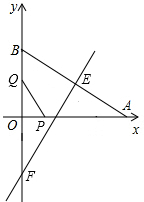 如图,在Rt△AOB中,∠AOB=90°,AO=$\sqrt{3}$,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.
如图,在Rt△AOB中,∠AOB=90°,AO=$\sqrt{3}$,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.