题目内容
已知:抛物线f:y=-(x-2)2+5,试写出把抛物线f向左平移2个单位后,所得的新抛物线f1的解析式,以及f关于x轴对称的曲线f2解析式,画出f1和f2的略图,并求:
(1)x的值在什么范围,抛物线f1和f2都是下降的;
(2)x的值在什么范围,曲线f1和f2围成一个封闭图形;
(3)求在f1和f2围成封闭图形上,平行于y轴的线段的长度的最大值.
(1)x的值在什么范围,抛物线f1和f2都是下降的;
(2)x的值在什么范围,曲线f1和f2围成一个封闭图形;
(3)求在f1和f2围成封闭图形上,平行于y轴的线段的长度的最大值.
考点:二次函数图象与几何变换
专题:
分析:根据平移规律和关于x轴对称的图象的特点求得f1和f2的解析式;
(1)根据抛物线的增减性回答问题;
(2)根据图象直接回答问题;
(3)封闭图形上,平行于y轴的线段的长度,就是对应于同一个横坐标,两曲线上的点的纵坐标的差.在区间-1≤x≤3内,设f1上的点P1(x,y1),f2上的点
P2(x,y2),求y1-y2的最大值,可用配方法.
(1)根据抛物线的增减性回答问题;
(2)根据图象直接回答问题;
(3)封闭图形上,平行于y轴的线段的长度,就是对应于同一个横坐标,两曲线上的点的纵坐标的差.在区间-1≤x≤3内,设f1上的点P1(x,y1),f2上的点
P2(x,y2),求y1-y2的最大值,可用配方法.
解答:解:∵抛物线f:y=-(x-2)2+5的顶点坐标是(2,5),
∴把抛物线f向左平移2个单位后的顶点坐标是(0,5),
∴抛物线f1:y=-x2+5.
又∵抛物线f与f2关于x轴对称,则抛物线f2:y=(x-2)2-5.
它们在平面直角坐标系中的大致图象如下:
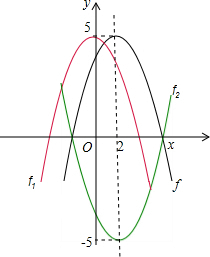
(1)根据图示知,当0<x<2时,曲线f1和f2都是下降的.
(2)依题意得-x2+5=(x-2)2-5,
整理,得
(x+1)(x-3)=0.
解得 x1=-1,x2=3.
则当-1≤x≤3时,曲线f1和f2围成一个封闭图形.
(3)设f1上的点P1(x,y1),f2上的点P2(x,y2),则
|y1-y2|=(-x2+5)-[(x-2)2-5]
=-2x2+4x+6
=-2(x-1)2+8.
∵-2<0,
∴|y1-y2|有最大值.
当x=1时,|y1-y2|的值最大是8.即线段长度的最大值是8.
∴把抛物线f向左平移2个单位后的顶点坐标是(0,5),
∴抛物线f1:y=-x2+5.
又∵抛物线f与f2关于x轴对称,则抛物线f2:y=(x-2)2-5.
它们在平面直角坐标系中的大致图象如下:

(1)根据图示知,当0<x<2时,曲线f1和f2都是下降的.
(2)依题意得-x2+5=(x-2)2-5,
整理,得
(x+1)(x-3)=0.
解得 x1=-1,x2=3.
则当-1≤x≤3时,曲线f1和f2围成一个封闭图形.
(3)设f1上的点P1(x,y1),f2上的点P2(x,y2),则
|y1-y2|=(-x2+5)-[(x-2)2-5]
=-2x2+4x+6
=-2(x-1)2+8.
∵-2<0,
∴|y1-y2|有最大值.
当x=1时,|y1-y2|的值最大是8.即线段长度的最大值是8.
点评:本题考查了二次函数图象的几何变换.对于函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程组求抛物线交点的坐标.

练习册系列答案
相关题目
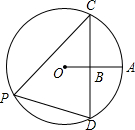 如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
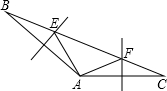 已知△ABC中,∠BAC=110°,AB、AC的垂直平分线分别交于BC于E,F,则∠EAF的度数( )
已知△ABC中,∠BAC=110°,AB、AC的垂直平分线分别交于BC于E,F,则∠EAF的度数( )| A、20° | B、40° |
| C、50° | D、60° |
 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E. 如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是
如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是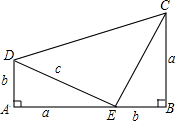 如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?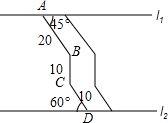 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.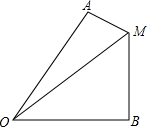 如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.
如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.