题目内容
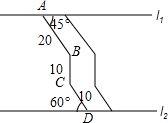 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.(1)求两景观长廊间的距离(结果保留根号);
(2)若通道的宽为1.5m,求出折线通道面积.
考点:解直角三角形的应用
专题:
分析:(1)作BN⊥l1,作CM⊥l2,在直角△ABH中利用三角函数求得BN的长,同理求得CM的长,BN+BC+CM就是所求;
(2)利用平行四边形的面积公式即可求解.
(2)利用平行四边形的面积公式即可求解.
解答: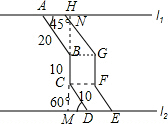 解:(1)作BN⊥l1,作CM⊥l2.
解:(1)作BN⊥l1,作CM⊥l2.
在直角△ABH中,BN=AB•sin∠HAB=20×
=10
(m).
同理,CM=CD•sin∠CDM=10×
=5
(m).
则MN=BN+BC+CM=10
+10+5
≈10×1.414+10(m).
即两景观长廊间的距离是10×1.414+10m;
(2)折线通道面积是:(20+10+10)×1.5=60(m2).
 解:(1)作BN⊥l1,作CM⊥l2.
解:(1)作BN⊥l1,作CM⊥l2.在直角△ABH中,BN=AB•sin∠HAB=20×
| ||
| 2 |
| 2 |
同理,CM=CD•sin∠CDM=10×
| ||
| 2 |
| 3 |
则MN=BN+BC+CM=10
| 2 |
| 3 |
即两景观长廊间的距离是10×1.414+10m;
(2)折线通道面积是:(20+10+10)×1.5=60(m2).
点评:本题考查了三角函数的应用以及平行四边形的面积公式,通过作辅助线转化为直角三角形的计算是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列各图形中,其中的一个三角形是由另一个三角形通过平移得到的是( )
A、 |
B、 |
C、 |
D、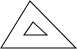 |
 根据市场调查,某种新产品投放市场30天内,每件产品的销售价格
根据市场调查,某种新产品投放市场30天内,每件产品的销售价格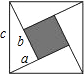 如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?
如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?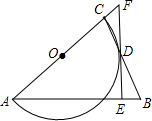 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.