题目内容
 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.(1)求证:0F⊥BD;
(2)若AB=
| 5 |
| 2 |
| ||
| 2 |
考点:圆周角定理
专题:
分析:(1)连接AF.根据直径所对的圆周角是直角、等腰三角形的性质以及平行线的性质即可证明;
(2)设AD=x.根据圆周角定理的推论和勾股定理进行求解.
(2)设AD=x.根据圆周角定理的推论和勾股定理进行求解.
解答:解:(1)证明:连接AF,如图所示: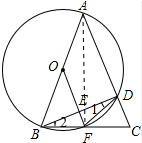
∵AB是⊙O的直径,
∴∠AFB=∠ADB=90°,
∵AB=AC,
∴FC=FB.
∵OA=OB,
∴OD∥AC.
∴∠OEB=∠ADB=90°,
∴OF⊥BD.
(2)设AD=x,
∵OF⊥BD,
∴可得OF是BD的中垂线,
∴FD=FB,
∴∠1=∠2,
∴BF=DF=
,
∵OF⊥DB,
∴ED=EB.
∴OE=
AE=
x,FE=OF-OE=
-
x,
在Rt△FEB中,BE2=EB2-FE2=(
)2-(
-
x)2;
在Rt△OFB中,BE2=OB2-OE2=(
)2-(
x)2;
∴(
)2-(
-
x)2=(
)2-(
x)2;
解得x=
,即AD=
.

∵AB是⊙O的直径,
∴∠AFB=∠ADB=90°,
∵AB=AC,
∴FC=FB.
∵OA=OB,
∴OD∥AC.
∴∠OEB=∠ADB=90°,
∴OF⊥BD.
(2)设AD=x,
∵OF⊥BD,
∴可得OF是BD的中垂线,
∴FD=FB,
∴∠1=∠2,
∴BF=DF=
| ||
| 2 |
∵OF⊥DB,
∴ED=EB.
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
在Rt△FEB中,BE2=EB2-FE2=(
| ||
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
在Rt△OFB中,BE2=OB2-OE2=(
| 5 |
| 4 |
| 1 |
| 2 |
∴(
| ||
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
解得x=
| 3 |
| 2 |
| 3 |
| 2 |
点评:此题考查了圆周角定理的推理、勾股定理以及等腰三角形的性质;培养学生综合运用定理进行推理和计算的能力.

练习册系列答案
相关题目
多项式x3-2x2+x-4与2x3-5x+6的和是( )
| A、3x3+2x2-4x+2 |
| B、3x3-2x2-4x+2 |
| C、-3x3+2x2-4x+2 |
| D、3x3-2x2-4x-2 |
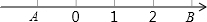 如图,在数轴上有A,B两点,A,B两点表示的有理数分别是a和b,a的倒数等于它本身,|b|=3,a<b且ab<0.
如图,在数轴上有A,B两点,A,B两点表示的有理数分别是a和b,a的倒数等于它本身,|b|=3,a<b且ab<0.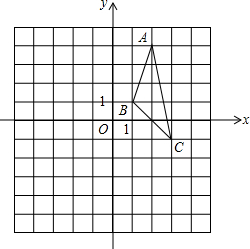 如图,在平面直角坐标系中,△ABC的三个顶点都在网格点上,回答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在网格点上,回答下列问题: 如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.
如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.