题目内容
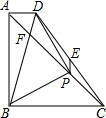 等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.
等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.(1)求证:AD⊥AB;
(2)连接DC,E为CD中点,连接PE,求证:AD=2PE;
(3)PE=1,PC=
| 2 |
考点:相似形综合题
专题:
分析:(1)根据∠BAC=∠BDP,∠AFB=∠DFP,证出△AFB∽△DFP,得出
=
,再根据∠AFD=∠BFP,证出△AFD∽△BFP,得出∠FAD=∠FBP=45°,∠BAD=90°,从而得出AD⊥AB;
(2)过点P作MN⊥AD的延长线于N,MN⊥BC于M,交DC于E′,过点C作CK⊥AD的延长线于K,DJ⊥AD,交AC于J,得出AD=DJ,四边形ABCK是正方形,四边形NMCK是矩形,△APB≌△APK,再证出PK=PB,PK=PD,DN=NK,根据△E′DN≌△E′MC,得出DE′=E′C,E、E′重合,根据PE∥DJ,ED=EC,得出JP=PC,PE=
DJ=
AD,从而证出AD=2PE;
(3)由(2)可知:AD=2PF=2,根据PC=
,求出MC=1,DN=NK=1,最后根据AB=AK即可得出答案.
| AF |
| FB |
| DF |
| FP |
(2)过点P作MN⊥AD的延长线于N,MN⊥BC于M,交DC于E′,过点C作CK⊥AD的延长线于K,DJ⊥AD,交AC于J,得出AD=DJ,四边形ABCK是正方形,四边形NMCK是矩形,△APB≌△APK,再证出PK=PB,PK=PD,DN=NK,根据△E′DN≌△E′MC,得出DE′=E′C,E、E′重合,根据PE∥DJ,ED=EC,得出JP=PC,PE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(2)可知:AD=2PF=2,根据PC=
| 2 |
解答:证明:
 (1)∵△ABC、△BDP是等腰直角三角形,
(1)∵△ABC、△BDP是等腰直角三角形,
∴∠BAC=∠BDP=45°,
∵∠AFB=∠DFP,
∴△AFB∽△DFP,
∴
=
,
∴
=
,
∵∠AFD=∠BFP,
∴△AFD∽△BFP,
∴∠FAD=∠FBP=45°,
∴∠BAD=90°,
∴AD⊥AB;
(2)过点P作MN⊥AD的延长线于N,MN⊥BC于M,交DC于E′,过点C作CK⊥AD的延长线于K,DJ⊥AD,交AC于J,
∵AD=DJ,四边形ABCK是正方形,四边形NMCK是矩形,△APB≌△APK,
∴PK=PB,
∵PB=PD,
∴PK=PD,
∵PN⊥DK,
∴DN=NK,
在△E′DN和△E′MC中,
,
∴△E′DN≌△E′MC,
∴DE′=E′C,
∴E、E′重合,
∵PE∥DJ,ED=EC,
∴JP=PC,
∴PE=
DJ=
AD,
∴AD=2PE;
(3)由(2)可知:AD=2PF=2,
∵PC=
,
∴MC=1,
∴DN=NK=1,
∴AB=AK=4.
 (1)∵△ABC、△BDP是等腰直角三角形,
(1)∵△ABC、△BDP是等腰直角三角形,∴∠BAC=∠BDP=45°,
∵∠AFB=∠DFP,
∴△AFB∽△DFP,
∴
| AF |
| DF |
| FB |
| FP |
∴
| AF |
| FB |
| DF |
| FP |
∵∠AFD=∠BFP,
∴△AFD∽△BFP,
∴∠FAD=∠FBP=45°,
∴∠BAD=90°,
∴AD⊥AB;
(2)过点P作MN⊥AD的延长线于N,MN⊥BC于M,交DC于E′,过点C作CK⊥AD的延长线于K,DJ⊥AD,交AC于J,
∵AD=DJ,四边形ABCK是正方形,四边形NMCK是矩形,△APB≌△APK,
∴PK=PB,
∵PB=PD,
∴PK=PD,
∵PN⊥DK,
∴DN=NK,
在△E′DN和△E′MC中,
|
∴△E′DN≌△E′MC,
∴DE′=E′C,
∴E、E′重合,
∵PE∥DJ,ED=EC,
∴JP=PC,
∴PE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=2PE;
(3)由(2)可知:AD=2PF=2,
∵PC=
| 2 |
∴MC=1,
∴DN=NK=1,
∴AB=AK=4.
点评:此题考查了相似形综合,用到的知识点是相似三角形和全等三角形的判定与性质、等腰直角三角形的性质,关键是根据题意做出辅助线,构造相似三角形.

练习册系列答案
相关题目
 如图,在△ABC中,斜边BC上的高AD=4,cosB=
如图,在△ABC中,斜边BC上的高AD=4,cosB=| 4 |
| 5 |
| A、6 | ||
B、
| ||
| C、5 | ||
| D、4 |
 已知,如图,在△ABC中,AB=AC,在AC上取点E,在AB的延长线上取点D,使BD=EC,连接DE交BC于点F.求证:DF=EF.
已知,如图,在△ABC中,AB=AC,在AC上取点E,在AB的延长线上取点D,使BD=EC,连接DE交BC于点F.求证:DF=EF. 如图,在矩形ABCD中,AM⊥BD,垂足为M,cos∠DAM=
如图,在矩形ABCD中,AM⊥BD,垂足为M,cos∠DAM= 如图,已知E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
如图,已知E、F是矩形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC. 如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.
如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.