题目内容
 如图,在△ABC中,斜边BC上的高AD=4,cosB=
如图,在△ABC中,斜边BC上的高AD=4,cosB=| 4 |
| 5 |
| A、6 | ||
B、
| ||
| C、5 | ||
| D、4 |
考点:解直角三角形
专题:
分析:根据直角三角形的性质,直角三角形的两个锐角互余,可得出∠B=∠CAD,再由AD=4,cosB=
,可得出AC的长.
| 4 |
| 5 |
解答:解:∵∠A=90°,AD为BC上的高,
∴∠BDA=90°,
∴∠B+∠BAD=∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵cosB=
,
∴cos∠CAD=
,
∴
=
,
∵AD=4,
∴AC=5,
故选C.
∴∠BDA=90°,
∴∠B+∠BAD=∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵cosB=
| 4 |
| 5 |
∴cos∠CAD=
| 4 |
| 5 |
∴
| AD |
| AC |
| 4 |
| 5 |
∵AD=4,
∴AC=5,
故选C.
点评:本题考查了解直角三角形,直角三角形的性质,直角三角形的两个锐角互余,熟练掌握三角函数的定义,是解题的关键.

练习册系列答案
相关题目
在下列多项式的乘法中,可用平方差公式计算的是( )
| A、(2+a)(a+2) | ||||
B、(
| ||||
| C、(-x+y)(y-x) | ||||
| D、(x2+y)(x-y2) |
在△ABC中,∠C=90°,若tanB=
,则sinA=( )
| 5 |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
要调查城区七年级10000名学生了解避险自救知识的情况.下列调查方式最合适的是( )
| A、在某校七年级学生中选取50名女生 |
| B、在某校七年级学生中选取50名男生 |
| C、在某校七年级学生中选取50名学生 |
| D、在城区10000名七年级学生中随机选取50名学生 |
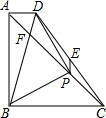 等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.
等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.