题目内容
 已知,如图,在△ABC中,AB=AC,在AC上取点E,在AB的延长线上取点D,使BD=EC,连接DE交BC于点F.求证:DF=EF.
已知,如图,在△ABC中,AB=AC,在AC上取点E,在AB的延长线上取点D,使BD=EC,连接DE交BC于点F.求证:DF=EF.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:作EG∥AB交BC于G,就可以得出∠EGC=∠ABC,∠DBF=∠EGF,∠D=∠GEF,就可以得出△DBF≌△EGF,就可以得出结论.
解答:解:作EG∥AB交BC于G,
则∠CGE=∠ABC,∠GEF=∠D,∠DBF=∠EGF.
∵AB=AC,
∴∠ABC=∠C,
∴∠C=∠EGC,
∴CE=EG,
∵CE=BD,
∴BD=GE.
在△DBF和△EGF中,
,
∴△DBF≌△EGF(ASA),
∴DF=EF.

则∠CGE=∠ABC,∠GEF=∠D,∠DBF=∠EGF.
∵AB=AC,
∴∠ABC=∠C,
∴∠C=∠EGC,
∴CE=EG,
∵CE=BD,
∴BD=GE.
在△DBF和△EGF中,
|
∴△DBF≌△EGF(ASA),
∴DF=EF.
点评:本题考查了等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定语言性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
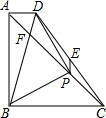 等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.
等腰Rt△ABC中,∠ABC=90°,且AB=BC,P为AC上一点,以BP为直角边向上作等腰Rt△BPD,∠BPD=90°.