题目内容
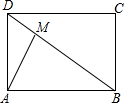如图，在矩形ABCD中，AM⊥BD，垂足为M，cos∠DAM=| 3 |
| 5 |
考点：矩形的性质,解直角三角形
专题：
分析：首先得出△ADM∽△BAM，进而利用相似三角形的性质表示出BM的长，进而利用勾股定理求出AD的长．
解答：解：∵AM⊥BD，垂足为M，cos∠DAM=
，
∴设AM=3x，AD=5x，则DM=4x，
∵∠DAM+∠BAM=90°，∠DAM+∠ADM=90°，
∴∠ADM=∠BAM，
又∵∠AMD=∠AMB，
∴△ADM∽△BAM，
∴
=
，
∴
=
，
解得：BM=
x，
∴BD=4x+
x=
x，
∵DC=4，
∴AD2+AB2=BD2，
即（5x）2+42=（
x）2
解得：x=
，
则AD的长为：5×
=
．
| 3 |
| 5 |
∴设AM=3x，AD=5x，则DM=4x，
∵∠DAM+∠BAM=90°，∠DAM+∠ADM=90°，
∴∠ADM=∠BAM，
又∵∠AMD=∠AMB，
∴△ADM∽△BAM，
∴
| AM |
| BM |
| DM |
| AM |
∴
| 3x |
| BM |
| 4x |
| 3x |
解得：BM=
| 9 |
| 4 |
∴BD=4x+
| 9 |
| 4 |
| 25 |
| 4 |
∵DC=4，
∴AD2+AB2=BD2，
即（5x）2+42=（
| 25 |
| 4 |
解得：x=
| 16 |
| 15 |
则AD的长为：5×
| 16 |
| 15 |
| 16 |
| 3 |
点评：此题主要考查了相似三角形的判定与性质以及勾股定理等知识，得出△ADM∽△BAM是解题关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
等腰Rt△ABC中，∠ABC=90°，且AB=BC，P为AC上一点，以BP为直角边向上作等腰Rt△BPD，∠BPD=90°．在下列多项式的乘法中，可用平方差公式计算的是（ ）
| A、（2+a）（a+2） | ||||
B、（
| ||||
| C、（-x+y）（y-x） | ||||
| D、（x2+y）（x-y2） |