题目内容
9.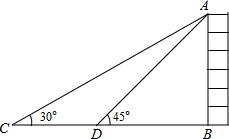 如图,如果在大厦AB所在的平地上选择一点C,测得大厦顶端A的仰角为30°,然后向大厦方向前进40米,到达点D处(C、D、B三点在同一直线上),此时测得大厦顶端A的仰角为45°,那么大厦AB的高度为20$\sqrt{3}$+20米(保留根号).
如图,如果在大厦AB所在的平地上选择一点C,测得大厦顶端A的仰角为30°,然后向大厦方向前进40米,到达点D处(C、D、B三点在同一直线上),此时测得大厦顶端A的仰角为45°,那么大厦AB的高度为20$\sqrt{3}$+20米(保留根号).
分析 先设AB=x;根据题意分析图形:本题涉及到两个直角三角形Rt△ACB和Rt△ADB,应利用其公共边BA构造等量关系,解三角形可求得DB、CB的数值,再根据CD=BC-BD=40,进而可求出答案.
解答 解:设AB=x,
在Rt△ACB和Rt△ADB中,
∵∠C=30°,∠ADB=45°,CD=40,
∴DB=x,AC=2x,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{3}$x,
∴∵CD=BC-BD=40,
$\sqrt{3}$x-x=40,
∴x=20($\sqrt{3}$+1),
故答案为:20$\sqrt{3}$+20.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念:仰角是向上看的视线与水平线的夹角,俯角是向下看的视线与水平线的夹角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
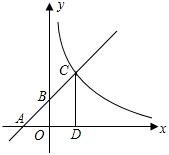 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(x>0)的图象在第一象限相交于点C,CD垂直于x轴,垂足为点D,若OA=OB=2,OD=1.
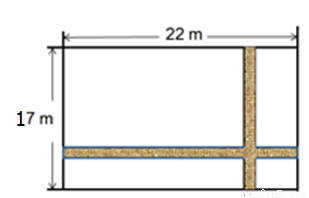
如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{m}{x}$(x>0)的图象在第一象限相交于点C,CD垂直于x轴,垂足为点D,若OA=OB=2,OD=1. ,则所修道路的宽度为( )m。
,则所修道路的宽度为( )m。