题目内容
13.已知二次函数f(x)满足f(2)=0,f(-1)=0且f(x)的最大值为9,求f(x)的解析式.分析 二次函数f(x)满足f(2)=0,f(-1)=0且f(x)的最大值为9,可知函数的顶点为($\frac{1}{2}$,9),设二次函数为f(x)=a(x-$\frac{1}{2}$)2+9,根据f(-1)=0可求得a.
解答 解:∵二次函数f(x)满足f(2)=0,f(-1)=0且f(x)的最大值为9,
∴二次函数f(x)的对称轴x=$\frac{2-1}{2}$=$\frac{1}{2}$,
∴顶点($\frac{1}{2}$,9),
设二次函数为f(x)=a(x-$\frac{1}{2}$)2+9,
由f(-1)=0得,a(-1-$\frac{1}{2}$)2+9=0,
解得a=4,
∴f(x)=4(x-$\frac{1}{2}$)2+9.
点评 本题考查了待定系数法求二次函数的解析式,根据题意求得顶点坐标是解题的关键.

练习册系列答案
相关题目
 如图所示,直线AB,CD相交于点O,已知∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠EOD和∠AOE的度数.
如图所示,直线AB,CD相交于点O,已知∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠EOD和∠AOE的度数. 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
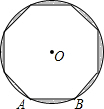 如图,AB为半径为2的⊙O的内接正八边形的一边,图中阴影部分的面积为4π-8$\sqrt{2}$.
如图,AB为半径为2的⊙O的内接正八边形的一边,图中阴影部分的面积为4π-8$\sqrt{2}$.
 如图所示,在1×2的正方形网格格点上已放置了两枚棋子,如果第三枚棋子随机放在其它格点上,那么以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为$\frac{3}{4}$.
如图所示,在1×2的正方形网格格点上已放置了两枚棋子,如果第三枚棋子随机放在其它格点上,那么以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为$\frac{3}{4}$.