Question

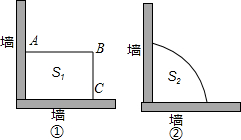
19．某农场计划建一个养鸡场，为了节约材料，决定利用原有的两面互相垂直的墙（墙足够长），另外的部分用30米的竹篱围成，现有两种方案：
①围成一个矩形（如图①）；
②围成一个$\frac{1}{4}$圆（如图②）．
设矩形的面积为S₁平方米，宽为x米，$\frac{1}{4}$圆的面积为S₂平方米，半径为r米．
请你通过计算帮助农场主选择一个围成区域面积最大的方案（π取3）．

Answer 1

分析 根据题意表示出矩形的长，进而利用配方法求出二次函数最值，再求出扇形半径，进而求出其面积．

解答 解：由题意可得：
方案一：设矩形的面积为S₁平方米，宽为x米，则另一边长为：（30-x）m，根据题意可得：
S₁=x（30-x）=-x²+30x=-（x-15）²+225；
方案二：设$\frac{1}{4}$圆的面积为S₂平方米，半径为r米，
则$\frac{90πr}{180}$=30，
则r=20，
根据题意可得：
S₂=$\frac{1}{4}$πr²=$\frac{1}{4}$×3×20²=300（平方米）．
答：方案二的面积较大．

点评 此题主要考查了二次函数的应用以及扇形面积求法，正确得出扇形半径是解题关键．