Question

4．如图，已知二次函数y=ax²+bx+c的图象过A（2，0），B（0，-1）和C（4，5）三点．
（1）求二次函数的解析式，对称轴，顶点坐标；
（2）画二次函数的图象并标出图象与x轴的另一个交点为D，求点D的坐标．

Answer 1

分析 （1）把A，B，C三点坐标代入二次函数解析式求出a，b，c的值，确定出二次函数解析式，进而求出对称轴与顶点坐标即可；
（2）画出二次函数图象，标出点D，求出D坐标即可．

解答 解：（1）把A（2，0），B（0，-1），C（4，5）代入得：$\left\{\begin{array}{l}{4a+2b+c=0}\\{c=-1}\\{16a+4b+c=5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\\{c=-1}\end{array}\right.$，
则二次函数解析式为y=$\frac{1}{2}$x²-$\frac{1}{2}$x-1=$\frac{1}{2}$（x-$\frac{1}{2}$）²-$\frac{9}{8}$，即对称轴为直线x=$\frac{1}{2}$，顶点坐标为（$\frac{1}{2}$，-$\frac{9}{8}$）；     
（2）如图所示：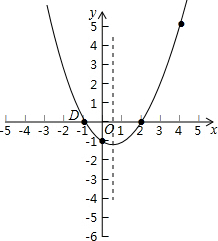

y=$\frac{1}{2}$x²-$\frac{1}{2}$x-1，令y=0，得到$\frac{1}{2}$x²-$\frac{1}{2}$x-1=0，
解得：x=2或x=-1，
则D（-1，0）．

点评 此题考查了抛物线与x轴的交点，二次函数的性质，以及待定系数法求二次函数解析式，熟练掌握二次函数的图象与性质是解本题的关键．