��Ŀ����
��֪������C1��y=x2+bx+c�Ķ���ΪP����y�ύ�ڵ�A����ֱ��OP���ڵ�B��
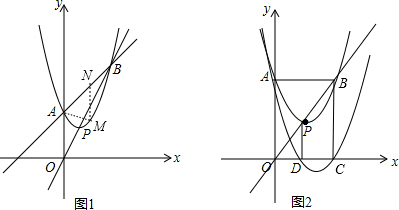
��1����ͼ1������P�ĺ�����Ϊ1����B������Ϊ��3��6������������C1�Ľ���ʽ��
��2������1���е�������C1��y������ƽ��3����λ���ȣ�Ȼ��������ƽ��m��m��0������λ���ȵõ�������C2��������C2��x�ύ�ڵ�C��D����C�ڵ�D����ࣩ����PD����P��������C1�Ķ��㣩������C��CN��PD��y�ύ�ڵ�N����tan��CNP=2����������C2�Ľ���ʽ��
��3����ͼ2������P�ڵ�һ���ޣ���PA=PO������P��PE��x���ڵ�E����������y=x2+bx+cƽ�ƣ�ƽ�ƺ�����������C3������A��E����������C3��x�����һ����ΪF����̽���ı���OABF����״����˵�����ɣ�

��1����ͼ1������P�ĺ�����Ϊ1����B������Ϊ��3��6������������C1�Ľ���ʽ��
��2������1���е�������C1��y������ƽ��3����λ���ȣ�Ȼ��������ƽ��m��m��0������λ���ȵõ�������C2��������C2��x�ύ�ڵ�C��D����C�ڵ�D����ࣩ����PD����P��������C1�Ķ��㣩������C��CN��PD��y�ύ�ڵ�N����tan��CNP=2����������C2�Ľ���ʽ��
��3����ͼ2������P�ڵ�һ���ޣ���PA=PO������P��PE��x���ڵ�E����������y=x2+bx+cƽ�ƣ�ƽ�ƺ�����������C3������A��E����������C3��x�����һ����ΪF����̽���ı���OABF����״����˵�����ɣ�

���㣺���κ����ۺ���
ר�⣺
��������1���������b��ֵ��Ȼ���b=-2����B��3��6����������������߽���ʽy=x2+bx+c���c��ֵ�������ߵĽ���ʽ���������
��2���ȸ���ƽ�Ƶ����ʵõ�������C2�Ľ���ʽΪy=��x-m��2+2-3=��x-m��2-1���ٸ���tan��CNP=2�������Ǻ���������⣻
��3����PA=PO��OA=c���ɵ�PD=
����֪������y=x2+bx+c�Ķ�������Ϊ P��-
��
�����������b��c�Ĺ�ϵ�������õ�A��0��
b2����P��-
b��
b2����D��-
b��0��������B����ֱ���������ߵĽ��㣬���B������꣬��ƽ�ƺ�������߾�����A������ƽ�ƺ�������߽���ʽΪy=x2+mx+
b2�������b��m֮��Ĺ�ϵ�������C������꣬�������Ա�ƽ������ȵ��ı�����ƽ���ı��Σ���ϡ�AOC=90�㼴��֤���ı���OABC�Ǿ��Σ�
��2���ȸ���ƽ�Ƶ����ʵõ�������C2�Ľ���ʽΪy=��x-m��2+2-3=��x-m��2-1���ٸ���tan��CNP=2�������Ǻ���������⣻
��3����PA=PO��OA=c���ɵ�PD=
| c |
| 2 |
| b |
| 2 |
| 4c-b2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
����⣺��1�������⣬-
=1��
���b=-2��
��b=-2����B��3��6����������������߽���ʽy=x2+bx+c��6=32-2��3+c��
��� c=3��
���������ߵĽ���ʽΪy=x2-2x+3��
��2���߽���1���е�������C1��y������ƽ��3����λ���ȣ�Ȼ��������ƽ��m��m��0������λ���ȵõ�������C2��
��y=��x-m��2+2-3=��x-m��2-1��
��tan��CNP=2��
��y=x2-��2+2
��x+5+2
��
 ��3����ͼ2���� PA=PO��OA=c���ɵ�PD=
��3����ͼ2���� PA=PO��OA=c���ɵ�PD=
��
��������y=x2+bx+c�Ķ�������Ϊ P��-
��
����
��
=
��b2=2c��
��������y=x2+bx+
b2��A��0��
b2����P��-
b��
b2����D��-
b��0����
�ɵ�ֱ��OP�Ľ���ʽΪy=-
bx��
�ߵ�B��������y=x2+bx+
b2��ֱ��y=-
bx��ͼ��Ľ��㣬
��-
bx=x2+bx+
b2��
���x1=-b��x2=-
��
�ɵõ�B������Ϊ��-b��
b2����
��ƽ�ƺ�������߾�����A������ƽ�ƺ�������߽���ʽΪy=x2+mx+
b2��
����D��-
b��0�����������y=x2+mx+
b2����m=
b��
��ƽ�ƺ�������߽���ʽΪy=x2+
bx+
b2��
��y=0����x2+
bx+
b2=0��
���x1=-b��x2=-
b��
�����⣬��C������Ϊ��-b��0����
��BC=
b2��
��BC=OA��
�֡�BC��OA��
���ı���OABC��ƽ���ı��Σ�
�ߡ�AOC=90�㣬
���ı���OABC�Ǿ��Σ�
| b |
| 2��1 |
���b=-2��
��b=-2����B��3��6����������������߽���ʽy=x2+bx+c��6=32-2��3+c��
��� c=3��
���������ߵĽ���ʽΪy=x2-2x+3��
��2���߽���1���е�������C1��y������ƽ��3����λ���ȣ�Ȼ��������ƽ��m��m��0������λ���ȵõ�������C2��
��y=��x-m��2+2-3=��x-m��2-1��
��tan��CNP=2��
��y=x2-��2+2
| 5 |
| 5 |
 ��3����ͼ2���� PA=PO��OA=c���ɵ�PD=
��3����ͼ2���� PA=PO��OA=c���ɵ�PD=| c |
| 2 |
��������y=x2+bx+c�Ķ�������Ϊ P��-
| b |
| 2 |
| 4c-b2 |
| 4 |
��
| 4c-b2 |
| 4 |
| c |
| 2 |
��b2=2c��
��������y=x2+bx+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
�ɵ�ֱ��OP�Ľ���ʽΪy=-
| 1 |
| 2 |
�ߵ�B��������y=x2+bx+
| 1 |
| 2 |
| 1 |
| 2 |
��-
| 1 |
| 2 |
| 1 |
| 2 |
���x1=-b��x2=-
| b |
| 2 |
�ɵõ�B������Ϊ��-b��
| 1 |
| 2 |
��ƽ�ƺ�������߾�����A������ƽ�ƺ�������߽���ʽΪy=x2+mx+
| 1 |
| 2 |
����D��-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��ƽ�ƺ�������߽���ʽΪy=x2+
| 3 |
| 2 |
| 1 |
| 2 |
��y=0����x2+
| 3 |
| 2 |
| 1 |
| 2 |
���x1=-b��x2=-
| 1 |
| 2 |
�����⣬��C������Ϊ��-b��0����
��BC=
| 1 |
| 2 |
��BC=OA��
�֡�BC��OA��
���ı���OABC��ƽ���ı��Σ�
�ߡ�AOC=90�㣬
���ı���OABC�Ǿ��Σ�
������������Ҫ������κ������ۺ����֪ʶ�������漰�����߽���ʽ���������߶�����Գ�������Լ����ε��ж����ر��ǵ�������Ƶ�ƽ�Ƶ�֪ʶ��ͬѧ������ʱ�����棬�����ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����AOB=��COD=90�㣬OCƽ�֡�AOB����DOE����BOE=2��3�������COE�Ķ�����
��ͼ����AOB=��COD=90�㣬OCƽ�֡�AOB����DOE����BOE=2��3�������COE�Ķ����� ��ͼ��Ϊ�˲���ij������CD�ĸ߶ȣ���ƽ����A����ý����ﶥ��C������Ϊ30�㣬��AD����ǰ��12����B������B����ý����ﶥ��C������Ϊ60�㣬������CD�ĸ߶�Ϊ��������
��ͼ��Ϊ�˲���ij������CD�ĸ߶ȣ���ƽ����A����ý����ﶥ��C������Ϊ30�㣬��AD����ǰ��12����B������B����ý����ﶥ��C������Ϊ60�㣬������CD�ĸ߶�Ϊ�������� ��֪Բ�İ뾶Ϊ4��Բ��ΪO����AOB=60�㣬������OAB�������
��֪Բ�İ뾶Ϊ4��Բ��ΪO����AOB=60�㣬������OAB������� ��ͼ�����߳�Ϊ1cm�ĵȱ�������ABC��ֱ��l���ҷ�����������������B�ӿ�ʼ��������������·���ij���Ϊ
��ͼ�����߳�Ϊ1cm�ĵȱ�������ABC��ֱ��l���ҷ�����������������B�ӿ�ʼ��������������·���ij���Ϊ ��ͼ����ֱ֪��y=
��ͼ����ֱ֪��y=