题目内容
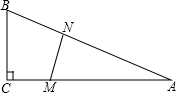 如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
如图,在△ABC中,∠C=90°,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.(1)当t为何值时,△AMN的面积为6米?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
考点:一元二次方程的应用,配方法的应用
专题:几何动点问题
分析:(1)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,根据△AMN的面积为6米,得到关于t的方程求得t值即可;
(2)根据三角形的面积计算得到有关t的二次函数求最值即可.
(2)根据三角形的面积计算得到有关t的二次函数求最值即可.
解答: 解:(1)在Rt△ABC中,
解:(1)在Rt△ABC中,
∵AB2=BC2+AC2
∴AB=5
米
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴
=
,
即:
=
,
∴NH=t,
∴S△AMN=
t(5
-t)=6,
解得t1=
,t2=4
(舍去),
故当t为
秒时,△AMN的面积为6米,
(2)
t(5
-t)=-
(t2-5
t+
)+
=-
(t-
)2+
,
∴当t=
时,S最大值=
平方米.
 解:(1)在Rt△ABC中,
解:(1)在Rt△ABC中,∵AB2=BC2+AC2
∴AB=5
| 3 |
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴
| AN |
| AB |
| NH |
| BC |
即:
| 2t |
| 10 |
| NH |
| 5 |
∴NH=t,
∴S△AMN=
| 1 |
| 2 |
| 3 |
解得t1=
| 3 |
| 3 |
故当t为
| 3 |
(2)
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 75 |
| 4 |
| 75 |
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
| 75 |
| 2 |
∴当t=
5
| ||
| 2 |
| 75 |
| 2 |
点评:本题考查了相似三角形的判定与性质,解题的关键是根据证得的相似三角形得到比例式,从而求解.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
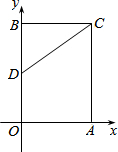 在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标分别为
在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标分别为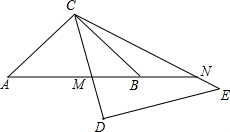 如图,等腰直角三角形ABC,AC=BC,若∠DCE=45°,且CD交AB于点M,CE交AB的延长线于点N,记AM=x,MN=y,BN=z,问以x,y,z为边长的三角形是怎样的三角形?并说明理由.
如图,等腰直角三角形ABC,AC=BC,若∠DCE=45°,且CD交AB于点M,CE交AB的延长线于点N,记AM=x,MN=y,BN=z,问以x,y,z为边长的三角形是怎样的三角形?并说明理由.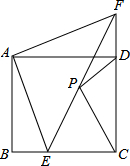 如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
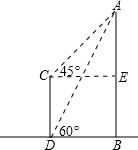 某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(
某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(