题目内容
3.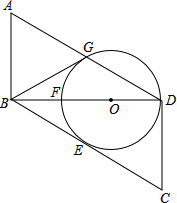 如图,在?ABCD中,对角线BD⊥CD,O为对角线BD上一点,以O为圆心的圆与BC相切于点E,交BD于点F,交AD于点G.
如图,在?ABCD中,对角线BD⊥CD,O为对角线BD上一点,以O为圆心的圆与BC相切于点E,交BD于点F,交AD于点G.(1)当∠C=60°时,判断直线BG与⊙O的位置关系,并说明理由;
(2)当G为AD中点时,若BG=$\sqrt{3}$,BF=1,求⊙O的半径.
分析 (1)BG是⊙O的切线.只要证明△BOG≌△BOE,即可推出∠BGO=∠BEO=90°,由此即可解决问题;
(2)设⊙O的半径为r.由△ODG∽△GDB,可得$\frac{OD}{DG}$=$\frac{DG}{BD}$,列出方程即可解决问题;
解答 解:(1)BG是⊙O的切线.
理由:连接OG、OE.
∵BC是⊙O的切线,
∴OE⊥BC,
∴∠OEC=90°,
∵四边形ABCD是平行四边形,AB⊥BD,
∴AB∥CD,∠A=∠C=60°,
∴∠ABD=∠CDB=∠OED=90°,
∴∠DOE=120°,∠ADB=30°,
∵OG=OD,
∴∠ODG=∠OGD=30°,
∴∠GOD=∠BOE=60°,
∵OB=OB,OG=OE,
∴△BOG≌△BOE,
∴∠BGO=∠BEO=90°,
∴BG⊥OG,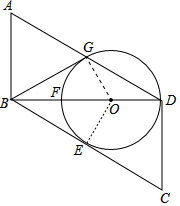
∴BG是⊙O的切线.
(2)设⊙O的半径为r.
∵∠ABD=90°,AG=GD,
∴GB=GD,
∴∠GBD=∠GDB,
∵OG=OD,
∴∠ODG=∠OGD=∠GBD,
∴△ODG∽△GDB,
∴$\frac{OD}{DG}$=$\frac{DG}{BD}$,
∴$\frac{r}{\sqrt{3}}$=$\frac{\sqrt{3}}{2r+1}$,
解得r=1或-$\frac{3}{2}$(舍弃),
∴⊙O的半径为1.
点评 本题考查切线的判定和性质、平行四边形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
11.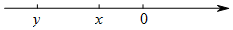 已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
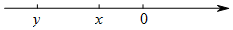 已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )
已知x,y两个实数在数轴上位置如图所示,则|y-x|+$\sqrt{{{(x-y)}^2}}$=( )| A. | 2x | B. | 2y | C. | 2x-2y | D. | 2y-2x |
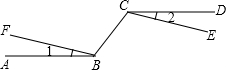 如图,AB∥CD,BF和CE是射线,且∠1=∠2,问BF与CE的位置有什么关系,说明理由.
如图,AB∥CD,BF和CE是射线,且∠1=∠2,问BF与CE的位置有什么关系,说明理由.