题目内容
15.在△ABC中,∠C=90°,AC=4,AB=5,现将△ABC绕点B逆时针旋转90°,若点C旋转后的对应点是C′,则CC′的长为3$\sqrt{2}$.分析 先根据勾股定理计算出BC=3,再根据旋转的性质得∠CBC′=90°,CB=C′B=3,然后再利用勾股定理可计算出CC′的长.
解答 解:如图,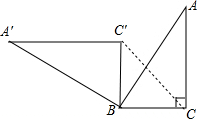 ∵∠C=90°,AC=4,AB=5,
∵∠C=90°,AC=4,AB=5,
∴BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵△ABC绕点B逆时针旋转90°,点C旋转后的对应点是C′,
∴∠CBC′=90°,CB=C′B=3,
∴CC′=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
故答案为3$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理.

练习册系列答案
相关题目
10.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
3.教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)间的关系为y=-$\frac{1}{12}$(x-4)2+3,由此可知铅球推出的距离是( )
| A. | 2m | B. | 8m | C. | 10m | D. | 12m |
20.已知x=-1是方程2x2+ax-5=0的一个根,则a的值是( )
| A. | -3 | B. | -4 | C. | 3 | D. | 7 |
 已知:线段a,b和c(如图),用直尺和圆规作△ABC,使BC=a,CA=b,AB=c.(请保留作图痕迹,不写作法)
已知:线段a,b和c(如图),用直尺和圆规作△ABC,使BC=a,CA=b,AB=c.(请保留作图痕迹,不写作法)