题目内容
18.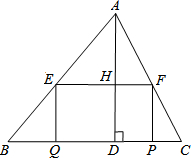 如图,在△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H,设ED=x.
如图,在△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H,设ED=x.(1)用含有x的代数式表示DH的长;
(2)当x为何值时,矩形EFPQ的面积最大?并求其最大值.
分析 (1)可以证明△AEF∽△ABC,根据相似三角形的对应高的比等于相似比即可用含有x的代数式表示DH的长;
(2)根据矩形的面积公式,可以把面积表示成关于EF的长的函数,根据函数的性质即可求解;
解答 解:(1)∵在矩形EFPQ中,EF∥PQ.
∴△AEF∽△ABC.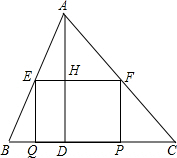
又∵AD⊥BC,
∴AH⊥EF.
∴$\frac{AH}{AD}=\frac{EF}{BC}$,
∴$\frac{8-DH}{8}=\frac{x}{10}$,
∴DH=8-$\frac{4}{5}$x;
(2)设矩形EFPQ的面积为y,
∴y=EF×DH=x(8-$\frac{4}{5}$x)=-$\frac{4}{5}$x2+8x=-$\frac{4}{5}$(x-5)2+20.
∵a=-$\frac{4}{5}$<0,
∴当x=5时,y的最大值为20.
点评 本题主要考查了相似三角形的性质与二次函数的应用,熟悉相似三角形的判定和性质是解决问题的关键.

练习册系列答案
相关题目
14.某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.

各年级学生人数统计表
请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校九年级学生比八年级学生少5人,请你补全上表,并利用样本数据估计全校三个年级学生中最喜欢跳绳运动的人数约为多少?

各年级学生人数统计表
| 年级 | 七年级 | 八年级 | 九年级 |
| 学生人数 | 180 | 165 | 160 |
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校九年级学生比八年级学生少5人,请你补全上表,并利用样本数据估计全校三个年级学生中最喜欢跳绳运动的人数约为多少?
 已知:线段a,b和c(如图),用直尺和圆规作△ABC,使BC=a,CA=b,AB=c.(请保留作图痕迹,不写作法)
已知:线段a,b和c(如图),用直尺和圆规作△ABC,使BC=a,CA=b,AB=c.(请保留作图痕迹,不写作法)
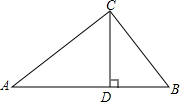 已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.
已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.