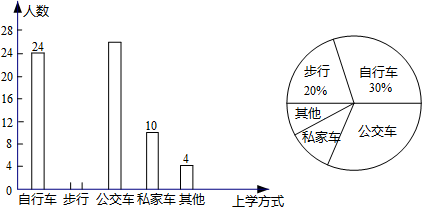
题目内容
10. 如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.
如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.(1)画出经过两次平移后的图形,并写出A1,B1,C1的坐标;
(2)已知三角形ABC内部一点P的坐标为(a,b),若点P随三角形ABC一起平移,请写出平移后点P的对应点P1的坐标;
(3)求三角形ABC的面积.
分析 (1)利用点平移的规律写出A1,B1,C1的坐标,然后描点可得△A1B1C1;
(2)利用点平移的规律,平移后的对应点的横坐标减3,纵坐标减4,于是可得P1(a-3,b-4);
(3)根据三角形面积公式,利用一个矩形的面积分别减去三个三角形的面积可求出三角形ABC的面积.
解答 解:(1)如图,△A1B1C1为所作,点A1,B1,C1的坐标分别为(-4,-3),(1,-2),(-1,1);
(2)平移后点P的对应点P1的坐标为(a-3,b-4);
(3)△ABC的面积=4×5-$\frac{1}{2}$×6×1-$\frac{1}{2}$×3×3-$\frac{1}{2}$×4×3=6.5.
点评 本题考查了作图-平移变换:确定平移后图形的基本要素(平移方向、平移距离).作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.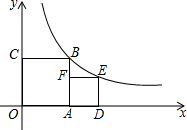 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )| A. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ | B. | $({\frac{{\sqrt{5}+1}}{2},\frac{{\sqrt{5}-1}}{2}})$ | C. | $({\frac{{\sqrt{5}}}{2},-\frac{{\sqrt{5}}}{2}})$ | D. | (1,1) |
20.下列事件属于必然事件的是( )
| A. | 地面往上抛出的篮球会落下 | B. | 软木塞沉在水底 | ||
| C. | 抛掷一枚硬币,落地后正面朝上 | D. | 买一张彩票中大奖 |
 如图,已知在三角形ABC中,∠A=56°,AB=8cm,BC=12cm,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,DF交AB于点G.
如图,已知在三角形ABC中,∠A=56°,AB=8cm,BC=12cm,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,DF交AB于点G. 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是(-505,505).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是(-505,505).