题目内容
14.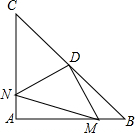 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.(1)写出点D到△ABC三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△DMN的形状,并证明你的结论.
分析 (1)根据直角三角形的性质可知CD=BD=AD;
(2)连接AD,可证明△ADM≌△CDN,则可证得DM=DN,∠CDN=∠ADM,再利用AD⊥BC,可求得ND⊥MD,可判定△DMN为等腰直角三角形.
解答 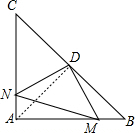 解:
解:
(1)∵在Rt△ABC中,∠BAC=90°,D为BC的中点,
∴CD=BD=AD,
即点D到三个顶点的距离相等;
(2)△DMN为等腰直角三角形,
证明如下:
如图,连接AD,
由(1)可知CD=AD,
∵AC=AB,
∴AD⊥BC,且∠DAB=∠CAD=45°,
∴∠C=∠DAM,
∵AN=BM,
∴CN=AM,
在△ADM和△CDN中
$\left\{\begin{array}{l}{AD=CD}\\{∠DAM=∠C}\\{AM=CN}\end{array}\right.$
∴△ADM≌△CDN(SAS),
∴DM=DN,且∠ADM=∠CDN,
∴∠ADM+∠ADN=∠ADN+∠NDC=90°,
∴△DMN为等腰直角三角形.
点评 本题主要考查等腰直角三角形、全等三角形的判定和性质,在(1)中掌握直角三角形斜边上的中线等于斜边的一半是解题的关键,在(2)中证明△ADM≌△CDN是解题的关键.

练习册系列答案
相关题目
5.若非零实数a、b满足4a2+b2=4ab,则$\frac{b}{a}$=( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
6.笔记本每本m元,买x本笔记本需( )
| A. | mx元 | B. | m 元 | C. | x元 | D. | m+x元 |
3.下列说法正确的是( )
| A. | 单项式3ab的次数是1 | |
| B. | 单项式$\frac{2ab}{3}$的系数是2 | |
| C. | 3a-2a2b+2ab是三次三项式 | |
| D. | -4a2b,3ab,5是多项式-4a2b+3ab-5的项 |
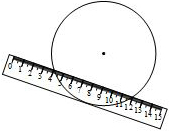 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm.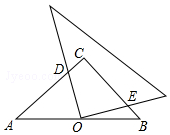 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.
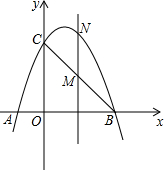 如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.