题目内容
8.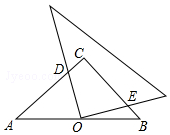 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=1.
分析 连接CO,结合等腰直角三角形的性质可证明△ADO≌△COE,可证得AD=CE,则可求得CD+CE=AC=1.
解答 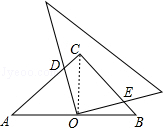 解:
解:
如图,连接CO,
∵在等腰直角△ABC中,∠C=90°,点O是AB的中点,
∴CO=AO,∠A=∠OCB=45°,且∠AOC=90°,
∵∠DOE=90°,
∴∠AOD+∠DOC=∠DOC+∠COE=90°,
∴∠AOD=∠COE,
在△ADO和△COE中
$\left\{\begin{array}{l}{∠A=∠OCE}\\{AO=CO}\\{∠AOD=∠COE}\end{array}\right.$
∴△ADO≌△COE(ASA),
∴AD=CE,
∴CD+CE=CD+AD=AC=1,
故答案为:1.
点评 本题主要考查等腰直角三角形的性质和全等三角形的判定和性质,连接OC,构造三角形全等,证得AD=CE是解题的关键.

练习册系列答案
相关题目
3.△ABC三边a,b,c满足a2+b+|$\sqrt{c-2}$-2|=10a+2$\sqrt{b-4}$-22,△ABC为( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
13. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,阴影部分面积S1+S2的大小变化情况是( )| A. | 一直不变 | B. | 一直减小 | C. | 一直增大 | D. | 先减小后增大 |
15.若x2-kx+16恰好是另一个整式的平方,则常数k的值为( )
| A. | ±4 | B. | +4 | C. | ±8 | D. | -8 |
 如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD于点H,DC=AH,连接AD、AC,点F在弦AE上,连接DF、CF,∠DFE=∠CAH,∠CFE=∠CAD,CH=$\sqrt{37}$,则AF长为5.
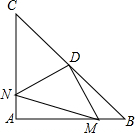 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.