题目内容
3.下列说法正确的是( )| A. | 单项式3ab的次数是1 | |
| B. | 单项式$\frac{2ab}{3}$的系数是2 | |
| C. | 3a-2a2b+2ab是三次三项式 | |
| D. | -4a2b,3ab,5是多项式-4a2b+3ab-5的项 |
分析 A、次数为所有字母的指数的和:1+1=2;
B、系数是数字因数,为$\frac{2}{3}$;
C、多项式中的最高次项的次数即为多项式的次数,所以-2a2b是三次,所以此多项式也是三次三项式;
D、-5丢了负号,每一项要包括它前面的符号.
解答 解:A、单项式3ab的次数是2,所以选项A,不符合题意;
B、单项式$\frac{2ab}{3}$的系数是$\frac{2}{3}$,所以选项B,不符合题意;
C、3a-2a2b+2ab是三次三项式,所以选项C,符合题意;
D、-4a2b,3ab,-5是多项式-4a2b+3ab-5的项,所以选项D,不符合题意;
故选C.
点评 此题考查了多项式和单项式,考查了多项式的项数及次数、单项式的系数和次数,熟练掌握这些定义是解本题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.下列运算正确的是( )
| A. | $\sqrt{8}$÷$\sqrt{2}$=2 | B. | 5$\sqrt{3}$•5$\sqrt{2}$=5$\sqrt{6}$ | C. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{6}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
18.下列各数是无理数的是( )
| A. | -0.101001 | B. | $\sqrt{7}$ | C. | $\frac{1}{4}$ | D. | 0 |
15.若x2-kx+16恰好是另一个整式的平方,则常数k的值为( )
| A. | ±4 | B. | +4 | C. | ±8 | D. | -8 |
12.要使分式$\frac{1}{{{x^2}-1}}$有意义,则x应满足的条件是( )
| A. | x≠1 | B. | x≠-1 | C. | x≠0 | D. | x≠±1 |
13.-2017的相反数是( )
| A. | -$\frac{1}{2017}$ | B. | $\frac{1}{2017}$ | C. | 7102 | D. | 2017 |

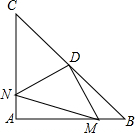 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.