题目内容
8．
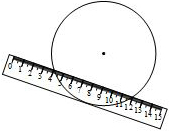如图，两边平行的刻度尺在圆上移动，当刻度尺的一边与直径为10cm的圆相切时，另一边与圆两个交点处的读数恰好为“4”和“12”（单位：cm），则刻度尺的宽为2cm．
分析 根据垂径定理得BE的长，再根据勾股定理列方程求解即可．
解答 解：作OE垂直AB于E交⊙O与D，
设OB=r，
根据垂径定理，BE=$\frac{1}{2}$AB=4，
根据题意列方程得：（5-DE）2+16=52，
解得：DE=2，
∴该直尺的宽度为2cm．
故答案为：2．
点评 此题主要考查了垂径定理的应用，此题很巧妙，将垂径定理和勾股定理不露痕迹的镶嵌在实际问题中，考查了同学们的转化能力．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
，0）、（3
，0）、（0，5），点D在第一象限，且∠ADB＝60º，则线段CD的长的最小值为______.
如图，在⊙O中，AB是直径，CD是弦，AB⊥CD于点H，DC=AH，连接AD、AC，点F在弦AE上，连接DF、CF，∠DFE=∠CAH，∠CFE=∠CAD，CH=$\sqrt{37}$，则AF长为5．
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列，若规定（m，n）表示第m排的第n个数，如（4，2）表示的数是 $\sqrt{6}$，则（5，4）与（18，15）表示的两数之积是2$\sqrt{3}$．
12．
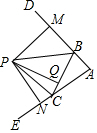如图，∠DBC和∠ECB是△ABC的两个外角，点P是∠DBC、∠ECB两角的平分线的交点，PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段，PM、PN、PQ的数量关系为（ ）
如图，∠DBC和∠ECB是△ABC的两个外角，点P是∠DBC、∠ECB两角的平分线的交点，PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段，PM、PN、PQ的数量关系为（ ）| A． | PM＞PN＞PQ | B． | PM＜PN＜PQ | C． | PM=PN=PQ | D． | PM=PN＞PQ |
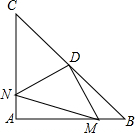如图，在Rt△ABC中，AB=AC，∠BAC=90°，D为BC的中点．