题目内容
6.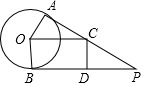 如图,PA、PB分别与⊙O相切于点A、B,过点O作OC∥BP交切线AP于C,在切线BP上截取BD=CP,连接CD.
如图,PA、PB分别与⊙O相切于点A、B,过点O作OC∥BP交切线AP于C,在切线BP上截取BD=CP,连接CD.(1)求证:四边形OCDB是矩形;
(2)若⊙O的半径R=1,PA=2+$\sqrt{3}$,求PA、PB与⊙O所围成的曲边三角形的面积.
分析 (1)连接OP,根据切线长定理得到∠APO=∠BPO,根据平行线的性质得到∠COP=∠BO,等量代换得到∠COP=∠CPO,得到OC=PC,根据矩形的判定定理即可得到结论;
(2)根据勾股定理得到OC=2,根据三角函数的定义得到∠AOB=150°,于是得到结论.
解答 解:(1)连接OP,
∵PA、PB分别与⊙O相切于点A、B,
∴∠APO=∠BPO,
∵BP∥OC,
∴∠COP=∠BO,
∴∠COP=∠CPO,
∴OC=PC,
∵BD=PC,
∴OC=BD,
∴四边形BDCO是平行四边形,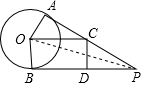
∵∠OBD=90°,
∴四边形OCDB是矩形;
(2)∵∠OAP=90°,OA=1,PA=2+$\sqrt{3}$,
∴AC=AP-CP=AP-OC,
∵AO2+AC2=OC2,
∴12+(2+$\sqrt{3}$-OC)2=OC2,
∴OC=2,
∴∠ACO=30°,
∴∠AOC=60°,
∴∠AOB=150°,
∴PA、PB与⊙O所围成的曲边三角形的面积=S四边形AOBP-S扇形AOB=1×(2+$\sqrt{3}$)-$\frac{150•π×{1}^{2}}{360}$=2+$\sqrt{3}$-$\frac{5}{12}$π.
点评 本题考查了切线的性质,矩形的判定和性质,勾股定理,等腰三角形的判定和性质,平行线的性质,熟练掌握切线的性质是解题的关键.

练习册系列答案
相关题目
18.若关于x的一元一次不等式组$\left\{\begin{array}{l}{2x-1>3(x-2)}\\{x<m}\end{array}\right.$的解集是x<5,则m的取值范围是( )
| A. | m≥5 | B. | m>5 | C. | m≤5 | D. | m<5 |
1.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2017=( )
| A. | (31,47) | B. | (31,48) | C. | (32,47) | D. | (32,48) |
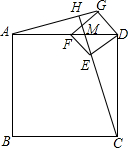 如图,已知正方形GFED的对角线DF在正方形ABCD的边DA上,连结AG,CE,并延长CE交AG于点H,若AD=4,DG=$\sqrt{2}$,则CE和CH的长分别是$\sqrt{10}$,$\frac{8\sqrt{10}}{5}$.
如图,已知正方形GFED的对角线DF在正方形ABCD的边DA上,连结AG,CE,并延长CE交AG于点H,若AD=4,DG=$\sqrt{2}$,则CE和CH的长分别是$\sqrt{10}$,$\frac{8\sqrt{10}}{5}$.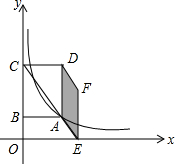 如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )
如图所示,在平面直角坐标系中,矩形ABCD的BC边落在y轴上,其它部分均在第一象限,双曲线y=$\frac{k}{x}$过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为( )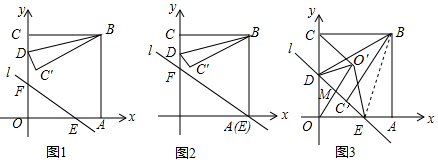
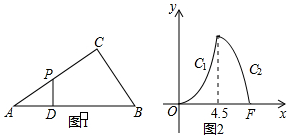 如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.
如图1,在Rt△ABC中,∠C=Rt∠,∠A=30°,D为AB上一个动点,过点D作DP⊥AB交折线A-C-B于点P,设AD的长为x,△APD的面积为y,y关于x的函数图象由C1,C2两段组成,如图2所示.