题目内容
14.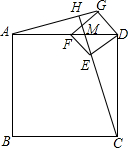 如图,已知正方形GFED的对角线DF在正方形ABCD的边DA上,连结AG,CE,并延长CE交AG于点H,若AD=4,DG=$\sqrt{2}$,则CE和CH的长分别是$\sqrt{10}$,$\frac{8\sqrt{10}}{5}$.
如图,已知正方形GFED的对角线DF在正方形ABCD的边DA上,连结AG,CE,并延长CE交AG于点H,若AD=4,DG=$\sqrt{2}$,则CE和CH的长分别是$\sqrt{10}$,$\frac{8\sqrt{10}}{5}$.
分析 根据全等三角形的性质得到得出∠DAG=∠DCE,而∠DCM+∠DMC=90°,从而∠DAG+∠AMH=90°,根据DG∥AC,得到△GAC与△DAC的面积相等,于是求出AG即可求出CH.
解答 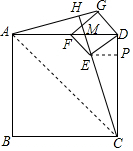 解:过点E作EP⊥CD于点P,连接AC,
解:过点E作EP⊥CD于点P,连接AC,
∵∠CDE+∠EDA=∠ADG+∠ADE=90°,
∴∠ADG=∠CDE,
在△ADG和△CDE中,$\left\{\begin{array}{l}{DG=DE}\\{∠ADG=∠CDE}\\{AD=CD}\end{array}\right.$,
∴△ADG≌△CDE(SAS),
∴∠DAG=∠DCE,
∵∠DCM+∠DMC=90°,
∴∠DAG+∠AMH=90°,
∴AG⊥CH;
∵∠EDF=∠EDC=45°,DG=$\sqrt{2}$,
∴DP=EP=1,
∵CD=AD=4,
∴CP=3,
∴CE=$\sqrt{10}$,
∴AG=$\sqrt{10}$,
∵∠DAC=∠ADG=45°,
∴DG∥AC,
∴S△AGC=S△ADC=$\frac{1}{2}$=8,
∵S△AGC=$\frac{1}{2}$AG•CH,
∴CH=$\frac{16}{\sqrt{10}}$=$\frac{8\sqrt{10}}{5}$.
故答案为:$\sqrt{10}$,$\frac{8\sqrt{10}}{5}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、三角形内角和性质、等积变换、勾股定理、平行四边形的判定与性质等知识点,难度较大.

练习册系列答案
相关题目
6.化简$\frac{{x}^{2}}{x-1}$+$\frac{1}{1-x}$的结果是( )
| A. | x+1 | B. | x-1 | C. | x2-1 | D. | $\frac{{x}^{2}+1}{x-1}$ |
5.下列事件中,属于必然事件的是( )
| A. | 你最喜欢的篮球队将夺得CBA冠军 | |
| B. | 打开电视,正在播《最强大脑》 | |
| C. | 任意买一张电影票,座位号是2的倍数 | |
| D. | 太阳从东方升起 |
9.函数y=3x-2的图象可由y=3x的图象( )得到.
| A. | 向左平移2个单位 | B. | 向右平移2个单位 | C. | 向上平移2个单位 | D. | 向下平移2个单位 |
19.下列方程中,属于二元一次方程的是 ( )
| A. | 2x-3y=z | B. | 5-x=$\frac{2}{y}$+1 | C. | x+y=0 | D. | 2 x2-x=5 |
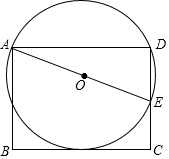 如图,点E为矩形ABCD中CD边上的一点,AB=3,AD=4,以AE为直径的⊙O恰好与BC边相切,则⊙O的半径为$\frac{13}{6}$.
如图,点E为矩形ABCD中CD边上的一点,AB=3,AD=4,以AE为直径的⊙O恰好与BC边相切,则⊙O的半径为$\frac{13}{6}$.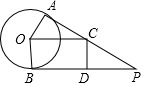 如图,PA、PB分别与⊙O相切于点A、B,过点O作OC∥BP交切线AP于C,在切线BP上截取BD=CP,连接CD.
如图,PA、PB分别与⊙O相切于点A、B,过点O作OC∥BP交切线AP于C,在切线BP上截取BD=CP,连接CD.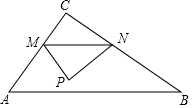 如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是相交.
如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是相交. 将一个正方体如图放置在一个长方体上,则所构成的几何体的左视图可能是( )
将一个正方体如图放置在一个长方体上,则所构成的几何体的左视图可能是( )


