题目内容
15.如图①,△ABC中,AB=AC,在BC上取BF=CE,求证:AE=AF.如图②,等边△DBE中,延长BD至点A,延长BE至点F,使DA=BF,求证:AE=AF.

分析 (1)只需证明△ABF≌△ACE即可.
(2)过点A作AM∥DE,延长BF交AM于点M,只需证明△ABE≌△AMF即可.
解答 (1)证明:∵△ABC中,AB=AC,
∴∠B=∠C=60°
在△ABF与△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠C=60°}\\{BF=CE}\end{array}\right.$
∴△ABF≌△ACE(SAS)
∴AE=AF
(2)如下图所示:
过点A作AM∥DE,延长BF交AM于点M,
∵△BDE是等边三角形,
∴∠BED=∠M=60°,△ABM是等边三角形,
∴AB=AM
∵DE∥AM,∠DAM=∠EMA=60°
∴四边形ADEM是等腰梯形,
∴AD=ME
又∵AD=BF,
∴BE=FM
在△ABE与△AMF中,$\left\{\begin{array}{l}{AB=AM}\\{∠B=∠M}\\{BE=MF}\end{array}\right.$
∴△ABE≌△AMF
∴AE=AF
点评 本题考查了全等三角形的判定与性质与等边三角形的性质,解题的关键是弄清楚需要证明的结论与全等三角形之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.定义一种新运算:a*b=ab-b2,如2*3=2×3-32=-3,则3*4的值为( )
| A. | 3 | B. | -4 | C. | 4 | D. | -3 |
4.拉动一个活动的长方形框架,将它拉成一个平行四边形.此时,平行四边形面积与原来长方形面积相比( )
| A. | 大一些 | B. | 相等 | C. | 小一些 | D. | 无法比较大小 |
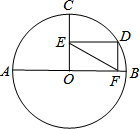 如图,AB为⊙O的直径,半径OC⊥AB,点D在$\widehat{BC}$上,DE⊥OC,DF⊥AB,垂足分别为E、F.若EF=5,则AB=10.
如图,AB为⊙O的直径,半径OC⊥AB,点D在$\widehat{BC}$上,DE⊥OC,DF⊥AB,垂足分别为E、F.若EF=5,则AB=10.
 如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC.
如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC.