题目内容
20.计算(1)$\sqrt{27}$-$\sqrt{\frac{1}{3}}$+$\sqrt{12}$
(2)(3+2$\sqrt{2}$)(2$\sqrt{2}$-3)
(3)$\frac{{\sqrt{15}+\sqrt{60}}}{{\sqrt{3}}}$-3$\sqrt{5}$
(4)|$\sqrt{2}$-2|+$\frac{{\sqrt{6}×\sqrt{3}}}{{\sqrt{2}}}$-($\sqrt{8}$-3)0.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式计算;
(3)先进行二次根式的除法运算,然后化简后合并即可;
(4)先根据二次根式的乘除法则和零指数幂的意义运算,然后去绝对值后合并即可.
解答 解:(1)原式=3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+2$\sqrt{3}$
=$\frac{14}{3}\sqrt{3}$;
(2)原式=8-9
=-1;
(3)原式=$\sqrt{\frac{15}{3}}$+$\sqrt{\frac{60}{3}}$-3$\sqrt{5}$
=$\sqrt{5}$+2$\sqrt{5}$-3$\sqrt{5}$
=0;
(4)原式=2-$\sqrt{2}$+$\sqrt{\frac{6×3}{2}}$-1
=2-$\sqrt{2}$+3-1
=4-$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
8.若二次函数y=x2+mx的对称轴是直线x=3,则m的值为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
12.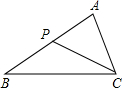 如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )
如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )
 如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )
如图,点P是△ABC的边AB上的一点,下列条件中不能得到△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}=\frac{AC}{AB}$ | D. | $\frac{AP}{AC}=\frac{PC}{CB}$ |

 如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC.
如图,已知等边△ABC,延长BC至D,E在AB上,使AE=CD,连接DE,交AC于F点,过E作EG⊥AC于G点.求证:FG=$\frac{1}{2}$AC. 根据立体图从上面看到的形状图(如图所示),画出它从正面和左面看到的形状图(图中数字代表该位置的小正方体的个数).
根据立体图从上面看到的形状图(如图所示),画出它从正面和左面看到的形状图(图中数字代表该位置的小正方体的个数).