题目内容
9.如图1,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针旋转30°,得到矩形EFGH(点E与O重合).(1)求点F的坐标,并判断点F是否在线段BC上;
(2)如图2,将矩形FEGH沿y轴向下平移m个单位,
①当四边形OFCE是平行四边形使,则m的值是多少?此时过点O作直线l将?OFCE分为面积比为1:3的两部分,求直线l的解析式;
②设矩形EFGH沿y轴向下平移过程中与矩形OABC重叠部分面积为S,写出S关于m的解析式,并求当S:S矩形ABCO=$\sqrt{3}$:6时m的值.

分析 (1)根据矩形的性质和等腰直角三角形的性质即可求得;
(2)①分两种情况,情形一:取CF的中点D1,作直线OD1根据${S}_{△OF{D}_{1}}$:${S}_{四边形O{D}_{1}CE}$=1:3即可求出点D1坐标,求出直线OD1;情形二:取EC中点D2,作直线OD2,则${S}_{△OE{D}_{2}}$:${S}_{四边形OFC{D}_{2}}$=1:3,先求出点D2坐标即可求出直线OD2.
②由OF∥E′F′得$\frac{CD}{CO}=\frac{CF′}{CF}$即$\frac{CD}{2}=\frac{2\sqrt{3}-m}{2\sqrt{3}}$,求出CD、CF′,列出方程即可解决.
解答 解:(1)如图1,过点F作FM⊥OA,垂足为M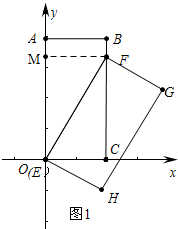
∵矩形OABC,点A(0,4),C(2,0),
∴B(2,4),
∴OF=OA=4,∠MOF=30°,
∴MF=$\frac{1}{2}$OF=2,OM=2$\sqrt{3}$,
∴F(2,2$\sqrt{3}$),
∴F在线段BC上;
(2)如图2中,①四边形OFCE是平行四边形,OE=FC,
∴可得:m=2$\sqrt{3}$-m,
解得:m=$\sqrt{3}$,
分两种情况,情形一:取CF的中点D1,作直线OD1,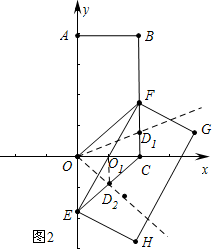
则${S}_{△OF{D}_{1}}$:${S}_{四边形O{D}_{1}CE}$=1:3
∵$FC=\sqrt{3}$,C(2,0),
∴D1(2,$\sqrt{3}$),
设直线OD1的解析式为y=kx,把D1(2,$\sqrt{3}$)代入得k=$\frac{\sqrt{3}}{4}$,
∴直线OD1为y=$\frac{\sqrt{3}}{4}$x.
情形二:取EC中点D2,作直线OD2,则${S}_{△OE{D}_{2}}$:${S}_{四边形OFC{D}_{2}}$=1:3,
设平行四边形的对角线交于点O1,
∵OC1=$\frac{1}{2}$OC=1,连接D2O1
∴O1D2=$\frac{1}{2}$OE=$\frac{\sqrt{3}}{2}$,D2O1∥OE,
∴D2O1⊥OC,
∴D2(1,$\frac{\sqrt{3}}{2}$),设直线OD2为y=k′x,把D2代入得到k′=-$\frac{\sqrt{3}}{2}$,
∴直线OD2为y=-$\frac{\sqrt{3}}{2}$x,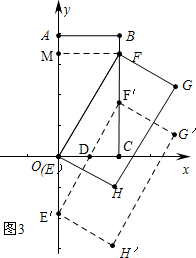
综上所述:所求直线l的解析式为y=$\frac{\sqrt{3}}{4}$x或y=-$\frac{\sqrt{3}}{2}$x.
②∵OF∥E′F′,
∴$\frac{CD}{CO}=\frac{CF′}{CF}$,
∴$\frac{CD}{2}=\frac{2\sqrt{3}-m}{2\sqrt{3}}$,
CD=$\frac{2\sqrt{3}-m}{\sqrt{3}}$,CF′=2$\sqrt{3}$-m,
∴S重合=$\frac{(2\sqrt{3}-m)^{2}}{2\sqrt{3}}$(0$≤m≤2\sqrt{3}$),
∵矩形OABC的面积为8,根据S重合:S矩形=$\sqrt{3}$:6得到S重合=$\frac{4\sqrt{3}}{3}$,
∴$\frac{(2\sqrt{3}-m)^{2}}{2\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,
解得m=2($\sqrt{3}-\sqrt{2}$)或【2($\sqrt{3}$+$\sqrt{2}$)不合题意舍弃】,
∴m=2($\sqrt{3}$-$\sqrt{2}$).
点评 本题考查矩形的性质,等腰直角三角形的性质、平移的性质等知识,考查学生运用性质进行推理的能力,解题的关键是通过特殊点“中点”的性质,解决了面积比的问题.

| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 55 |
| B型 | 50 | 70 |
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )| A. | 64 | B. | 16 | C. | 24 | D. | 32 |
| A. | 5a+a=5a2 | B. | 5a+b=5ab | C. | 5a2b-3ab2=2a2b | D. | 2ab2-5b2a=-3ab2 |
| A. | x=1,y=2 | B. | x=2,y=-1 | C. | x=0,y=2 | D. | x=3,y=1 |
 如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.
如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.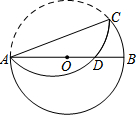 已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.
已知:如图,在半径为8的⊙O中,AB为直径,以弦AC(非直径)为对称轴将$\widehat{AC}$折叠后与AB相交于点D,如果AD=3DB,那么AC的长为4$\sqrt{14}$.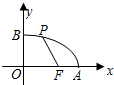 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.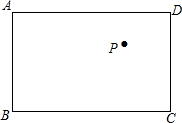 如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.
如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.