题目内容
19.抛物线y=-3(x+$\frac{1}{2}$)2是由抛物线y=-3x2向左平移$\frac{1}{2}$个单位得到.分析 根据向左平移横坐标减求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可.
解答 解:∵抛物线y=-3x2向左平移$\frac{1}{2}$个单位的顶点坐标为(-$\frac{1}{2}$,0),
∴得到新的图象的解析式y=-3(x+$\frac{1}{2}$)2.
故答案为:y=-3(x+$\frac{1}{2}$)2.
点评 本题考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式的变化更简便.

练习册系列答案
相关题目
14.对于抛物线y=x2+2和y=x2的论断:①开口方向不同;②形状完全相同;③对称轴相同.其中正确的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11.某商场计划购进A、B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
(1)若商场预计进货款为3900元,则这两种台灯各购进多少盏?
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 55 |
| B型 | 50 | 70 |
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
17. 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )| A. | 64 | B. | 16 | C. | 24 | D. | 32 |
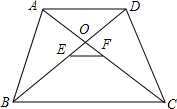 如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).
如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).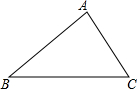 小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.