题目内容
2.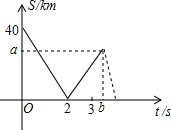 A、B两地之间路程是350km,甲、乙两车从A地以各自的速度匀速行驶到B地,甲车先出发半小时,乙车到达B地后原地休息等待甲车到达.如图是甲、乙两车之间的路程S(km)与乙车出发时间t(h)之间的函数关系的图象.
A、B两地之间路程是350km,甲、乙两车从A地以各自的速度匀速行驶到B地,甲车先出发半小时,乙车到达B地后原地休息等待甲车到达.如图是甲、乙两车之间的路程S(km)与乙车出发时间t(h)之间的函数关系的图象.(1)求甲、乙两车的速度;
(2)求图中a、b的值.
分析 (1)由“速度=路程÷时间”可得出甲车的速度,设乙车的速度为xkm/h,由“两车间的距离=速度差×时间”可得出关于x的一元一次方程,解方程即可求出甲车的速度;
(2)由“时间=两地间距÷时间”得出乙车到达B地的时间(即b值),再由“两车间距离=乙车行驶的路程-甲车行驶的路程”可得出当乙车到达B地时两车之间的距离(即a的值).
解答 解:(1)甲车的速度为:40÷0.5=80(km/h);
设乙车的速度为xkm/h,则2(x-80)=40,
解得:x=100.
答:甲车的速度为80km/h,乙车的速度为100km/h.
(2)b=350÷100=3.5;
a=350-80×(3.5+0.5)=30.
答:a的值为30,b的值为3.5.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系找出关于速度x的一元一次方程;(2)观察图形结合数量关系列式计算即可得出结论.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(或方程组)是关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
10.将代数式x2+6x-3化为(x+p)2+q的形式,正确的是( )
| A. | (x+3)2+6 | B. | (x-3)2+6 | C. | (x+3)2-12 | D. | (x-3)2-12 |
17.下列运算正确的是( )
| A. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | B. | $\sqrt{2}$+1=$\sqrt{3}$ | C. | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ | D. | 6$\sqrt{2}$+$\sqrt{2}$=7$\sqrt{2}$ |
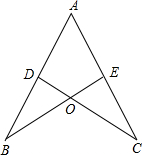 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. 如图,有一条公共边的正六边形和正方形如图放置,则∠α=150度.
如图,有一条公共边的正六边形和正方形如图放置,则∠α=150度. 如图,AB是⊙O的直径,弦CD∥AB,若∠ABD=60°,则∠ADC的度数是30°.
如图,AB是⊙O的直径,弦CD∥AB,若∠ABD=60°,则∠ADC的度数是30°.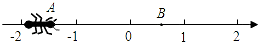 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则(m-1)(m-3)的值为1.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则(m-1)(m-3)的值为1.