题目内容
11. 如图,AB是⊙O的直径,弦CD∥AB,若∠ABD=60°,则∠ADC的度数是30°.
如图,AB是⊙O的直径,弦CD∥AB,若∠ABD=60°,则∠ADC的度数是30°.
分析 利用圆周角定理和直角三角形的两个锐角互余的性质求得∠DAB=25°;然后根据平行线的性质、等量代换可以求得∠ADC的度数.
解答 解:∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
又∵∠ABD=60°,
∴∠DAB=30°(直角三角形的两个锐角互余);
又∵CD∥AB,
∴∠ADC=∠DAB(两直线平行,内错角相等),
∴∠ADC=30°(等量代换).
故答案为:30°.
点评 本题综合考查了圆周角定理、平行线的性质.在圆中,直径所对的圆周角是直角.

练习册系列答案
相关题目
19.下列性质中,菱形具有但矩形不一定具有的是( )
| A. | 对边相等 | B. | 对边平行 | C. | 对角相等 | D. | 对角线互相垂直 |
6.调查某一路口某时段的汽车流量,记录了30天同一时段通过该路口的汽车辆数,其中有2天是256辆,2天是285辆,23天是899辆,3天是447辆.那么这30天在该时段通过该路口的汽车平均辆数为( )
| A. | 125辆 | B. | 320辆 | C. | 770辆 | D. | 900辆 |
5.若x+y=3,x-y=1,则x2-y2的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |
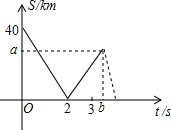 A、B两地之间路程是350km,甲、乙两车从A地以各自的速度匀速行驶到B地,甲车先出发半小时,乙车到达B地后原地休息等待甲车到达.如图是甲、乙两车之间的路程S(km)与乙车出发时间t(h)之间的函数关系的图象.
A、B两地之间路程是350km,甲、乙两车从A地以各自的速度匀速行驶到B地,甲车先出发半小时,乙车到达B地后原地休息等待甲车到达.如图是甲、乙两车之间的路程S(km)与乙车出发时间t(h)之间的函数关系的图象.