题目内容
19．已知关于x、y的方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$，a为常数．（1）求方程组的解；
（2）若方程组的解x＞y＞0，求a的取值范围．
分析 （1）根据加减法，可得方程组的解；
（2）根据解不等式组，可得不等式组的解集．
解答 解：（1）方程组中两式相加，得
3x=6a+3，
解得x=2a+1，
把x=2a+1代入2x+y=5a，解得y=a-2，
方程组的解为$\left\{\begin{array}{l}{x=2a+1}\\{y=a-2}\end{array}\right.$；
（2）由题意，得
$\left\{\begin{array}{l}{2a+1＞a-2}\\{a-2＞0}\\{2a+1＞0}\end{array}\right.$解得a＞2．
点评 本题考查了二元一次方程组的解，利用方程组的解得出不等式组是解题关键．
练习册系列答案
相关题目
9．
| 计算（写出计算步骤）： （1）$\frac{3}{4}-\frac{5}{12}+1\frac{5}{6}$； | （2）1-$\frac{3}{8}÷3×\frac{2}{3}$； | （3）$（\frac{14}{15}-\frac{7}{24}）×\frac{3}{2}$． |
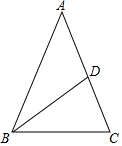如图所示，在△ABC中，AB=AC，AC边上的中线把三角形的周长分为18cm和30cm的两部分，求三角形各边的长．
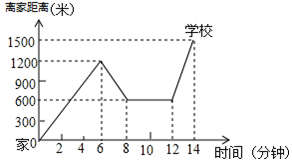“珍重生命，注意安全！”同学们在上下学途中一定要注意骑车安全．小明骑单车上学，当他骑了一段时间，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校，以下是他本次所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：
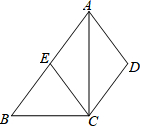如图，在四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．如果点E是AB的中点，AC=4，EC=2.5，写出求四边形ABCD的面积的思路．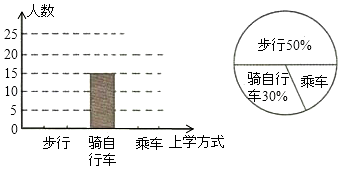
如图，已知∠AOB和线段CD，求作一点P，使PC=PD，并且点P到∠AOB的两边距离相等．（尺规作图，不写作法，保留作图痕迹）