题目内容
20.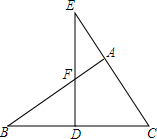 如图所示,在△ABC中,∠BAC=90°,D是边BC上的一点,过点D作ED⊥BC于点D,交CA的延长线于点E,交AB于点F,试找出图中的相似三角形,并用相似符号表示.
如图所示,在△ABC中,∠BAC=90°,D是边BC上的一点,过点D作ED⊥BC于点D,交CA的延长线于点E,交AB于点F,试找出图中的相似三角形,并用相似符号表示.
分析 由垂线的定义得出∠CDE=∠BDF=90°,得出∠BAV=∠CDE,∠EAF=90°,由∠C=∠C,∠E=∠E,∠B=∠B,得出△ABC∽△DEC,△AEF∽△DEC,△DBF∽△ABC,即可得出结果.
解答 解:△ABC∽△DEC∽△AEF∽△DBF.理由如下:
∵ED⊥BC,
∴∠CDE=∠BDF=90°,
∵∠BAC=90°,
∴∠BAV=∠CDE,∠EAF=90°,
∵∠C=∠C,∠E=∠E,∠B=∠B,
∴△ABC∽△DEC,△AEF∽△DEC,△DBF∽△ABC,
∴△ABC∽△DEC∽△AEF∽△DBF.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,由两角相等证明三角形相似是常用的判定方法,特别注意公共角的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列运算结果错误的是( )
| A. | -xy+xy=0 | B. | 4x-2x=2x | C. | 5x2y-6x2y=1 | D. | 2xy-yx=xy |
 如图所示,已知△ABC,过点A作直线l,求作△A′B′C′,使它与△ABC关于l对称,写出作图步骤并作图.
如图所示,已知△ABC,过点A作直线l,求作△A′B′C′,使它与△ABC关于l对称,写出作图步骤并作图. 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BD=BC,AD=DE=BE,试求△ABC各内角的度数.
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BD=BC,AD=DE=BE,试求△ABC各内角的度数.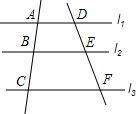 已知,如图,l1∥l2∥l3,下列等式:①$\frac{AB}{AC}$=$\frac{AD}{CF}$;②$\frac{BC}{CA}$=$\frac{EF}{FD}$;③$\frac{AB}{DE}$=$\frac{DF}{AC}$;④$\frac{AB}{DE}$=$\frac{AD}{BE}$;⑤AB:BC:AC=DE:EF:DF,成立的有( )
已知,如图,l1∥l2∥l3,下列等式:①$\frac{AB}{AC}$=$\frac{AD}{CF}$;②$\frac{BC}{CA}$=$\frac{EF}{FD}$;③$\frac{AB}{DE}$=$\frac{DF}{AC}$;④$\frac{AB}{DE}$=$\frac{AD}{BE}$;⑤AB:BC:AC=DE:EF:DF,成立的有( )