题目内容
15. 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BD=BC,AD=DE=BE,试求△ABC各内角的度数.
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BD=BC,AD=DE=BE,试求△ABC各内角的度数.
分析 根据等腰三角形的性质得到∠A=∠3,∠1=∠2,∠BDC=∠C,∠ABC=∠C,然后由三角形的外角的性质和三角形的内角和列方程即可得到结论.
解答 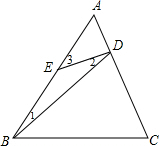 解:∵AD=DE,
解:∵AD=DE,
∴∠A=∠3,
∵DE=BE,
∴∠1=∠2,
∴∠A=2∠1,
∵BD=BC,
∴∠BDC=∠C,
∴∠C=∠1+∠A=3∠1,
∵AB=AC,
∴∠ABC=∠C=3∠1,
∵∠A+∠ABC+∠C=180°,
∴2∠1+3∠1+3∠1=180°,
∴∠1=22.5°,
∴∠A=45°,
∠ABC=∠C=67.5°.
点评 本题考查了三角形的内角和定理,等边对等角和三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
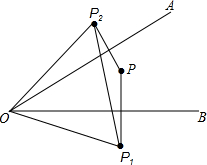 如图,已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称.求证:点P1,O,P2三点所构成的三角形是等边三角形.
如图,已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称.求证:点P1,O,P2三点所构成的三角形是等边三角形.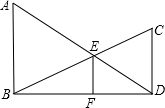 如图,AB⊥BD,CD⊥BD,B、D是垂足,AD和BC交于E,EF⊥BD于F.求证:$\frac{DE}{AD}$+$\frac{BE}{BC}$=1.
如图,AB⊥BD,CD⊥BD,B、D是垂足,AD和BC交于E,EF⊥BD于F.求证:$\frac{DE}{AD}$+$\frac{BE}{BC}$=1.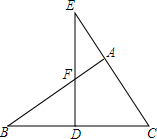 如图所示,在△ABC中,∠BAC=90°,D是边BC上的一点,过点D作ED⊥BC于点D,交CA的延长线于点E,交AB于点F,试找出图中的相似三角形,并用相似符号表示.
如图所示,在△ABC中,∠BAC=90°,D是边BC上的一点,过点D作ED⊥BC于点D,交CA的延长线于点E,交AB于点F,试找出图中的相似三角形,并用相似符号表示. 如图,四边形ABCD中,AD∥BC,AB=AD,求证:∠ABD=∠CBD.
如图,四边形ABCD中,AD∥BC,AB=AD,求证:∠ABD=∠CBD.