题目内容
为使关于x的一元二次方程x2-4ax+5a2-6a=0的两个实数根的差的绝对值最大,a的值应为 .
考点:二次函数的最值,根与系数的关系
专题:计算题
分析:设方程两个根为:x1,x2,根据根与系数的关系,则可得:x1+x2=4a,x1x2=5a2-6a,先求出差绝对值的最大值,即可求出a的值.
解答:解:设方程两个根为:x1,x2,根据根与系数的关系,则可得:x1+x2=4a,x1x2=5a2-6a,
∴(x1-x2)2=(x1+x2)2-4x1x2,
=16a2-20a2+24a,
=-4a2+24a,
=-4(a-3)2+36,
当a=3时,两个实数根的差的绝对值最大值为36.
故答案为:3.
∴(x1-x2)2=(x1+x2)2-4x1x2,
=16a2-20a2+24a,
=-4a2+24a,
=-4(a-3)2+36,
当a=3时,两个实数根的差的绝对值最大值为36.
故答案为:3.
点评:本题考查了二次函数最值及根与系数的关系,难度不大,关键是掌握用配方法求二次函数的最值.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
自圆外一点P引圆的两条割线PAB、PCD,连接AC、BD、AD、BC,则图中相似三角形的对数是( )
| A、2对 | B、3对 | C、4对 | D、5对 |
与在数轴上表示数2的点距离等于3个单位的点所表示的数是( )
| A、-1 | B、5 |
| C、3或-3 | D、-1或5 |
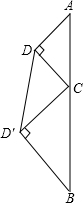 如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为
如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为 如图△ABC中,∠B=45°,∠C=a(a>45°),AD是BC边上的高,E是AD上一点且DE=DC,延长BE交AC于F,∠ABF的大小是
如图△ABC中,∠B=45°,∠C=a(a>45°),AD是BC边上的高,E是AD上一点且DE=DC,延长BE交AC于F,∠ABF的大小是