题目内容
 如图,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP•PC的值是( )
如图,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP•PC的值是( )| A、16 | B、20 | C、25 | D、30 |
考点:勾股定理
专题:
分析:过点A作AD⊥BC于D,根据等腰三角形的性质可得BD=CD,然后用BD、PD表示出BP、PC,整理并根据勾股定理可得AP2+BP•PC=AB2,代入数据计算即可得解.
解答: 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD,
∴BP=BD-PD,PC=CD+PD=BD+PD,
∴AP2+BP•PC=AP2+(BD-PD)(BD+PD),
=AP2+BD2-PD2,
在Rt△APD中,AP2-PD2=AD2,
∴AP2+BP•PC=BD2+AD2,
在Rt△ABD中,BD2+AD2=AB2=42=16,
即AP2+BP•PC=16.
故选A.
 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,∵AB=AC,
∴BD=CD,
∴BP=BD-PD,PC=CD+PD=BD+PD,
∴AP2+BP•PC=AP2+(BD-PD)(BD+PD),
=AP2+BD2-PD2,
在Rt△APD中,AP2-PD2=AD2,
∴AP2+BP•PC=BD2+AD2,
在Rt△ABD中,BD2+AD2=AB2=42=16,
即AP2+BP•PC=16.
故选A.
点评:本题考查了勾股定理,等腰三角形三线合一的性质,作辅助线构造出直角三角形是解题的关键,难点在于用BD、PD表示出BP、PC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
化简:(1+
)÷
的结果为( )
| 1 |
| x |
| x2-1 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
 一个正方体的平面展开图如图,将它折成正方体后,“建”字的对面是( )
一个正方体的平面展开图如图,将它折成正方体后,“建”字的对面是( )| A、和 | B、谐 | C、海 | D、南 |
 马航MH370航班于2014年3月8日凌晨与地面失去了联系,至今尚未找到有关马航MH370的任何消息.我国在第一时间派出了飞机和船只进行寻找.如图,某日在马航MH370失联的附近海域有两艘自西向东航行的海监船A、B正在执行搜索任务,B船在A船的正东方向,且两船保持20海里的距离,某一时刻在海监船A的东北方向,B的北偏东15°方向的我国渔政执法船C侦测到了疑似物品,上级命令B船马上前去支援,已知B船的速度是30海里/小时,求B船到达C船的时间是多少.(结果保留根号)
马航MH370航班于2014年3月8日凌晨与地面失去了联系,至今尚未找到有关马航MH370的任何消息.我国在第一时间派出了飞机和船只进行寻找.如图,某日在马航MH370失联的附近海域有两艘自西向东航行的海监船A、B正在执行搜索任务,B船在A船的正东方向,且两船保持20海里的距离,某一时刻在海监船A的东北方向,B的北偏东15°方向的我国渔政执法船C侦测到了疑似物品,上级命令B船马上前去支援,已知B船的速度是30海里/小时,求B船到达C船的时间是多少.(结果保留根号)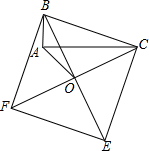 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0.如果AB=3,AO=2,那么AC的长等于
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0.如果AB=3,AO=2,那么AC的长等于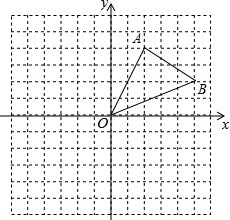 如图,三角形AOB中,A,B两点的坐标分别为(2,4)、(5,2).
如图,三角形AOB中,A,B两点的坐标分别为(2,4)、(5,2).